题目内容
20．下列直线中，与直线2x+y+1=0平行且与圆x2+y2=5相切的是（ ）| A． | 2x+y+5=0 | B． | x-2y+5=0 | C． | $2x+y+5\sqrt{5}=0$ | D． | $x-2y+5\sqrt{5}=0$ |
分析 设直线方程为2x+y+c=0，圆心到直线的距离d=$\frac{|c|}{\sqrt{5}}$=$\sqrt{5}$，求出c，可得结论．
解答 解：设直线方程为2x+y+c=0，圆心到直线的距离d=$\frac{|c|}{\sqrt{5}}$=$\sqrt{5}$，
∴c=±5，
故选A．
点评 本题考查直线方程，考查直线与圆的位置关系，比较基础．
练习册系列答案
阅读快车系列答案
相关题目
10．命题“?x∈R，x3-3x＞0”的否定为（ ）
| A． | ?x∈R，x3-3x≤0 | B． | ?x∈R，x3-3x＜0 | C． | ?x∈R，x3-3x≤0 | D． | ?x∈R，x3-3x＞0 |
11．圆（x-1）2+y2=1的圆心和半径分别为（ ）
| A． | （0，1），1 | B． | （0，-1），1 | C． | （-1，0），1 | D． | （1，0），1 |
8．已知双曲线的焦点在x轴上，焦距为2$\sqrt{5}$，且双曲线的一条渐近线与直线x-2y+1=0平行，则双曲线的标准方程为（ ）
| A． | $\frac{{x}^{2}}{4}$-y2=1 | B． | x2-$\frac{{y}^{2}}{4}$=1 | C． | $\frac{3{x}^{2}}{20}$-$\frac{3{y}^{2}}{5}$=1 | D． | $\frac{3{x}^{2}}{5}$-$\frac{3{y}^{2}}{20}$=1 |
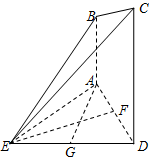如图，在平面ABCD中，AB⊥平面ADE，CD⊥平面ADE，△ADE是等边三角形，AD=DC=2AB=2，F，G分别为AD，DE的中点．
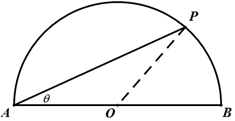运动员小王在一个如图所示的半圆形水域（O为圆心，AB是半圆的直径）进行体育训练，小王先从点A出发，沿着线段AP游泳至半圆上某点P处，再从点P沿着弧PB跑步至点B处，最后沿着线段BA骑自行车回到点A处，本次训练结束．已知OA=1500m，小王游泳、跑步、骑自行车的平均速度分别为2m/s，4m/s，10m/s，设∠PAO=θrad．
10．经过点$（{\frac{1}{2}，\frac{{\sqrt{3}}}{2}}）$的圆x2+y2=1的切线方程是（ ）
| A． | $x+\sqrt{3}y=2$ | B． | $\sqrt{3}x+y=2$ | C． | $x+\sqrt{3}y=1$ | D． | $\sqrt{3}x+y=1$ |