已知函数f(x)=e2x+x2.则f'(0)=2．题目和参考答案——青夏教育精英家教网——

题目内容

12．已知函数f（x）=e^2x+x²，则f'（0）=2．

分析先求出f′（x）=2e^2x+2x，由此能求出f'（0）．

解答解：∵函数f（x）=e^2x+x²，
∴f′（x）=2e^2x+2x，
∴f'（0）=2e^2×0+2×0=2．
故答案为：2．

点评本题考查导数值的求法，是基础题，解题时要认真审题，注意导数性质的合理运用．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

2．若实数x，y满足$\left\{\begin{array}{l}{2x+y-7≤0}\\{x≥2}\\{y≥1}\end{array}\right.$，则目标函数z=-x+y的最小值为（　　）

3．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$经过点D（0，1），一个焦点与短轴的两端点连线互相垂直．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过$M（0，-\frac{1}{3}）$的直线l交椭圆C于A，B两点，判断点D与以AB为直径的圆的位置关系，并说明理由．

20．下列直线中，与直线2x+y+1=0平行且与圆x²+y²=5相切的是（　　）

$2x+y+5\sqrt{5}=0$

$x-2y+5\sqrt{5}=0$

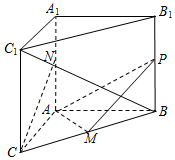如图，在三棱柱ABC-A₁B₁C₁中，AA₁⊥底面ABC，∠BAC=90°，AB=AC=2，$A{A_1}=\sqrt{3}$．M，N分别为BC和AA₁的中点，P为侧棱BB₁上的动点．
（Ⅰ）求证：平面APM⊥平面BB₁C₁C；
（Ⅱ）若P为线段BB₁的中点，求证：CN∥平面AMP；
（Ⅲ）试判断直线BC₁与PA能否垂直．若能垂直，求出PB的值；若不能垂直，请说明理由．

17．（1）已知抛物线y²=2px（p＞0）的焦点在直线2x-y-4=0上，求p的值；
（2）已知双曲线的渐近线方程为$y=±\frac{3}{4}x$，准线方程为$x=±\frac{16}{5}$，求双曲线的标准方程．

4．若复数z满足|z|=1（i为虚数单位），则|z-2i|的最小值是1．

1．已知二次函数f（x）=ax²-（2a-1）x-lnx（a为常数，a≠1）．
（Ⅰ）当a＜0时，求函数f（x）在区间[1，2]上的最大值；
（Ⅱ）记函数y=f（x）图象为曲线C，设点A（x₁，y₁），B（x₂，y₂）是曲线C上不同的两点，点M为线段AB的中点，过点M作x轴的垂线交曲线C于点N．判断曲线C在点N处的切线是否平行于直线AB？并说明理由．

6．当双曲线M：$\frac{{x}^{2}}{{m}^{2}}$-$\frac{{y}^{2}}{2m+6}$=1（-2≤m＜0）的焦距取得最小值时，双曲线M的渐近线方程为（　　）

y=±$\sqrt{2}$x

y=±$\frac{\sqrt{2}}{2}$x

y=±$\frac{1}{2}$x