题目内容
6.已知函数f(x)=|2x-3|-|x+1|.(1)若不等式f(x)≤a的解集是空集,求实数a的取值范围;
(2)若存在x0∈R,使得2f(x0)≤-t2+4|t|成立,求实数t的取值范围.
分析 (1)通过讨论x的范围,求出各个区间上的函数的最小值,求出f(x)的最小值,求出a的范围即可;
(2)求出f(x)的最小值,问题转化为-t2+4|t|+5≥0,求出t的范围即可.
解答 解:(1)x≥$\frac{3}{2}$时,f(x)=2x-3-x-1=x-4,
此时,f(x)的最小值是f($\frac{3}{2}$)=-$\frac{5}{2}$,
-1≤x≤$\frac{3}{2}$时,f(x)=3-2x-x-1=-3x+2,
此时,f(x)的最小值是f($\frac{3}{2}$)=-$\frac{5}{2}$,
x≤-1时,f(x)=3-2x+x+1=-x+4,
此时,f(x)的最小值是f(-1)=5,
综上,f(x)的最小值是-$\frac{5}{2}$,
若不等式f(x)≤a的解集是空集,
则a<-$\frac{5}{2}$;
(2)若存在x0∈R,使得2f(x0)≤-t2+4|t|成立,
只需求出f(x)的最小值,由(1)f(x)的最小值是-$\frac{5}{2}$,
问题转化为-t2+4|t|+5≥0,
即t2-4|t|-5≤0,即(|t|-5)(|t|+1)≤0,
解得:-5≤t≤5.
点评 本题考查了解绝对值不等式问题,考查分类讨论思想,转化思想,是一道中档题.

练习册系列答案
相关题目
1.在复平面中,复数$\frac{1}{{{{({1+i})}^2}+1}}+i$对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.已知2-9,2a1,2a2,2-1成等比数列,2,log3b1,log3b2,log3b3,0成等差数列,则b2(a2-a1)=( )
| A. | -8 | B. | 8 | C. | $-\frac{9}{8}$ | D. | $\frac{9}{8}$ |

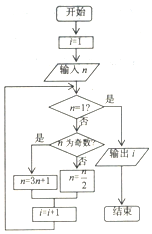 20世纪70年代,流行一种游戏---角谷猜想,规则如下:任意写出一个自然数n,按照以下的规律进行变换:如果n是个奇数,则下一步变成3n+1;如果n是个偶数,则下一步变成$\frac{n}{2}$,这种游戏的魅力在于无论你写出一个多么庞大的数字,最后必然会落在谷底,更准确的说是落入底部的4-2-1循环,而永远也跳不出这个圈子,下列程序框图就是根据这个游戏而设计的,如果输出的i值为6,则输入的n值为( )
20世纪70年代,流行一种游戏---角谷猜想,规则如下:任意写出一个自然数n,按照以下的规律进行变换:如果n是个奇数,则下一步变成3n+1;如果n是个偶数,则下一步变成$\frac{n}{2}$,这种游戏的魅力在于无论你写出一个多么庞大的数字,最后必然会落在谷底,更准确的说是落入底部的4-2-1循环,而永远也跳不出这个圈子,下列程序框图就是根据这个游戏而设计的,如果输出的i值为6,则输入的n值为( )