题目内容
1.在复平面中,复数$\frac{1}{{{{({1+i})}^2}+1}}+i$对应的点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 利用复数代数形式的乘除运算求出复数所对应点的坐标得答案.
解答 解:∵$\frac{1}{{{{({1+i})}^2}+1}}+i$=$\frac{1}{1+2i}+i=\frac{1-2i}{(1+2i)(1-2i)}+i$=$\frac{1}{5}+\frac{3}{5}i$.
∴复数$\frac{1}{{{{({1+i})}^2}+1}}+i$对应的点的坐标为($\frac{1}{5},\frac{3}{5}$),在第一象限.
故选:A.
点评 本题考查复数代数形式的乘除运算,考查复数的代数表示法及其几何意义,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.若z∈C,i为虚数单位,且$\frac{z}{{|z{|^2}}}=\frac{3}{5}-\frac{4}{5}i$,则复数z等于( )
| A. | $\frac{3}{5}+\frac{4}{5}i$ | B. | $\frac{3}{5}-\frac{4}{5}i$ | C. | $\frac{5}{3}-\frac{5}{4}i$ | D. | $\frac{4}{5}-\frac{3}{5}i$ |
9.已知向量$\overrightarrow m=(1,2)$,$\overrightarrow n=(2,3)$,则$\overrightarrow m$在$\overrightarrow n$方向上的投影为( )
| A. | $\sqrt{13}$ | B. | 8 | C. | $\frac{{8\sqrt{5}}}{5}$ | D. | $\frac{{8\sqrt{13}}}{13}$ |
16.“¬p为真”是“p∨q为假”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
13.已知实数a,b满足(a+i)(1-i)=3+bi(i为虚数单位),记z=a+bi,则|z|是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 5 | D. | 25 |
7.若某几何体的三视图(单位:cm)如图所示,则此几何体的侧面积等于( )
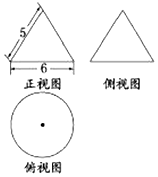

| A. | 12πcm2 | B. | 15πcm2 | C. | 24πcm2 | D. | 30πcm2 |
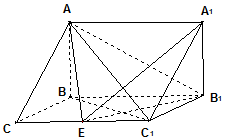 在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,∠BCC1=$\frac{π}{3}$,AB=CC1=2.
在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,∠BCC1=$\frac{π}{3}$,AB=CC1=2.