题目内容
18.已知三棱锥A-BCD中,AB=AC=3,BD=CD=$\sqrt{2}$,且BD⊥CD,若点A在平面BCD内的投影恰好为点D,则此三棱锥外接球的表面积为11π.分析 三棱锥A-BCD的三条侧棱两两互相垂直,所以把它扩展为长方体,它也外接于球,对角线的长为球的直径,然后解答即可.
解答 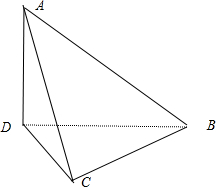 解:∵点A在平面BCD内的投影恰好为点D,∴AD⊥平面BCD,
解:∵点A在平面BCD内的投影恰好为点D,∴AD⊥平面BCD,
故AD=$\sqrt{A{B}^{2}-B{D}^{2}}=\sqrt{7}$,且知AD,BD,CD两两垂直,
故可将此三棱锥放入一个长、宽、高分别为$\sqrt{2}$,$\sqrt{2}$,$\sqrt{7}$的长方体内,三棱锥的四个顶点亦为长方体的顶点,其外接球为长方体外接球.
易得外接球半径为$\frac{\sqrt{11}}{2}$,故外接球表面积为11π.
故答案为:11π
点评 本题考查球的表面积,考查学生空间想象能力,解答的关键是构造球的内接长方体.是基础题

练习册系列答案
相关题目
13.在等比数列{an}中,已知${a_1}+{a_2}=-\frac{3}{2},{a_4}+{a_5}=12$,则数列是( )
| A. | 递增数列 | B. | 递减数列 | C. | 摆动数列 | D. | 常数列 |
7.棱长为4的正方体的内切球的表面积为( )
| A. | 4π | B. | 12π | C. | 16π | D. | 20π |
8.某同学的父亲决定今年夏天卖西瓜赚钱,根据去年6月份的数据统计连续五天内每天所卖西瓜的个数与温度之间的关系如表:
(1)求这五天内所卖西瓜个数的平均值和方差;
(2)求变量x.y之间的线性回归方程,并预测当温度为30℃时所卖西瓜的个数.
附:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$(精确到0.1)
| 温度x(℃) | 32 | 33 | 35 | 37 | 38 |
| 西瓜个数y | 20 | 22 | 24 | 30 | 34 |
(2)求变量x.y之间的线性回归方程,并预测当温度为30℃时所卖西瓜的个数.
附:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$(精确到0.1)
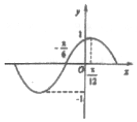 函数f(x)=sin(ωx+φ)(ω<0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将y=f(x)的图象向右平移$\frac{π}{4}$个单位长度后得到函数y=g(x)的图象.
函数f(x)=sin(ωx+φ)(ω<0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将y=f(x)的图象向右平移$\frac{π}{4}$个单位长度后得到函数y=g(x)的图象.