题目内容
15.已知函数f(x)=|x+3|-|x+a|是R上的奇函数.(1)求实数a的值;
(2)画出函数f(x)的图象;
(3)写出函数f(x)的值域.
分析 (1)根据函数为奇函数,得到f(0)=0,得a=-3,
(2)化为分段函数,画图即可,
(3)由图象可得得到答案.
解答 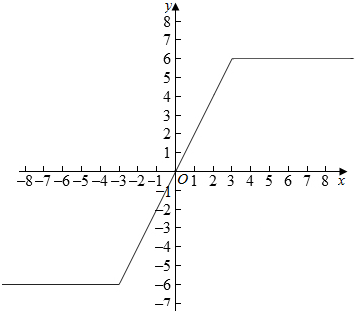 解:(1)∵f(x)=|x+3|-|x+a|是R上的奇函数.
解:(1)∵f(x)=|x+3|-|x+a|是R上的奇函数.
∴f(0)=0,得a=-3,
当a=-3时,f(x)=|x+3|-|x-3|,
f(-x)=|-x+3|-|-x-3|=|x-3|-|x+3|=-f(x),满足题意
∴a=-3,
(2)$f(x)=\left\{\begin{array}{l}-6,x<-3\\ 2x,-3≤x<3\\ 6,x≥3\end{array}\right.$,如图所示.
(3)由图象可知f(x)的值域是[-6,6].
点评 本题考查了函数的奇偶性,函数图象的画法,以及函数的值域,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.组合数$C_n^m+2C_n^{m-1}+C_n^{m-2}$(n≥m≥2,m,n∈N*)恒等于( )
| A. | $C_{n+2}^m$ | B. | $C_{n+2}^{m+1}$ | C. | $C_{n+1}^m$ | D. | $C_{n+1}^{m+1}$ |