题目内容
12.已知函数f(x)=x3-3ax-1,a≠0,若f(x)在x=-1处取极值(1)求a的值;
(2)若g(x)=f(x)-m有3个零点,求m的取值范围.
分析 (1)利用函数f(x)在x=-1处取得极值,求出a;
(2)若g(x)=f(x)-m有3个零点,只需直线y=m与y=f(x)的图象有三个不同的交点,则说明m小于极大值,大于极小值.
解答 解:(1)函数的导数为f'(x)=3x2-3a,因为f(x)在x=-1处取得极值,
所以f'(-1)=0,即3-3a=0,解得a=1.
(2)由(1)得:f(x)=x3-3x-1,
f'(x)=3x2-3=3(x2-1)=3(x-1)(x+1),
当f'(x)>0,得x>1或x<-1.当f'(x)<0,得-1<x<1.
即函数在x=-1处取得极大值f(-1)=1,在x=1处取得极小值f(1)=-3,
如图示: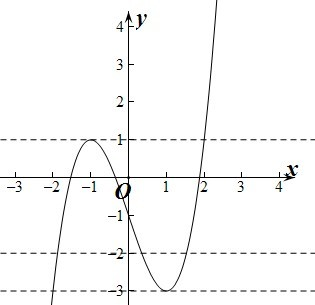 ,
,
若g(x)=f(x)-m有3个零点,
只需直线y=m与y=f(x)的图象有三个不同的交点,
则m小于极大值,大于极小值,
即-3<m<1,所以m的取值范围是(-3,1).
点评 本题的考点是利用导数研究函数的极值,以及函数的交点问题.要注意利用数形结合的数学思想去解决.

练习册系列答案
相关题目
3.若事件A与B互斥,已知P(A)=P(B)=$\frac{1}{4}$,则P(A∪B)的值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{16}$ | D. | 0 |
7.${∫}_{-a}^{a}$x[f(x)+f(-x)]dx等于( )
| A. | 4${∫}_{0}^{a}$xf(x)dx | B. | 2${∫}_{0}^{a}$x[f(x)+f(-x)]dx | C. | 0 | D. | 以上都不正确 |
1.设函数y=f(x)在(-∞,+∞)内有定义,对于给定的正数k,定义函数:${f_k}(x)=\left\{\begin{array}{l}f(x)(f(x)≤k)\\ k\;\;\;\;\;\;(f(x)>k)\end{array}\right.$,取函数f(x)=2-x-e-x,若对任意的x∈(-∞,+∞),恒有fk(x)=f(x),则( )
| A. | k的最大值为2 | B. | k的最小值为2 | C. | k的最大值为1 | D. | k的最小值为1 |
2.设x,y满足约束条件$\left\{{\begin{array}{l}{x+y≤3}\\{x-y≥-1}\\{y≥1}\end{array}}\right.$若0≤ax+by≤2恒成立,则a2+b2的最大值是( )
| A. | 1 | B. | $\frac{8}{9}$ | C. | $\frac{20}{9}$ | D. | 4 |