题目内容

7．${∫}_{-a}^{a}$x[f（x）+f（-x）]dx等于（　　）
A．4${∫}_{0}^{a}$xf（x）dxB．2${∫}_{0}^{a}$x[f（x）+f（-x）]dxC．0D．以上都不正确

分析 令g（x）=x[f（x）+f（-x）]，由定义可知函数g（x）为[-a，a]上的奇函数，再由奇函数在对称区间上的定积分为0得答案．

解答 解：令g（x）=x[f（x）+f（-x）]，
则g（-x）=-x[f（-x）+f（x）]=-g（x），
则函数g（x）为[-a，a]上的奇函数，
∴${∫}_{-a}^{a}$x[f（x）+f（-x）]dx=0．
故选：C．

点评 本题考查定积分，明确奇函数在对称区间上的定积分为0是关键，是基础题．

练习册系列答案
相关题目
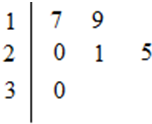17．某车间共有12名工人，随机抽取6名，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数．
（Ⅰ） 根据茎叶图计算样本均值；
（Ⅱ） 日加工零件个数大于样本均值的工人为优秀工人．根据茎叶图推断该车间12名工人中有几名优秀工人；
（Ⅲ）在（Ⅱ）的条件下，从该车间12名工人中，任取2人，记取出的2人中优秀工人的人数为随机变量ξ，求ξ的期望．
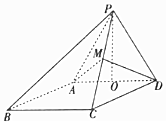18．如图，四棱锥P-ABCD，底面ABCD是∠ABC=60°的菱形，侧面PAD是边长为2的正三角形，O是AD的中点，M为PC的中点．
（1）求证：PC⊥AD；
（2）若PO与底面ABCD垂直，求直线DM与平面PAC所成的角的正弦值．
15．已知函数f（x）=ex-x+a，g（x）=$\frac{1}{{e}^{x}}$+x+a2，a∈R．
（1）求函数f（x）的单调区间；
（2）若存在x∈[0，2]，使得f（x）＜g（x）成立，求a的取值范围；
（3）设x1，x2是函数f（x）的两个不同零点，求证：e${\;}^{{x}_{1}+{x}_{2}}$＜1．
2．设二次函数f（x）=ax2+bx+c在区间[-2，2]上的最大值、最小值分别是M、m，集合A={x|f（x）=x}．
（1）若A={1，2}，且f（0）=2，求M和m的值；
（2）若A={1}，且a≥1，记g（a）=M+m，求g（a）的最小值．
12．已知函数f（x）=x3-3ax-1，a≠0，若f（x）在x=-1处取极值
（1）求a的值；
（2）若g（x）=f（x）-m有3个零点，求m的取值范围．
19．（1）求函数y=2x-$\sqrt{x-1}$的值域；
（2）求函数y=$\frac{3x-1}{x+1}$的值域．
16．已知椭圆$\frac{x^2}{4}+\frac{y^2}{20}$=1的焦点坐标为  （　　）
A．（±4，0）B．（±2，0）C．（0，±4）D．（0，±2）
17．已知关于x的一元二次方程x2-2ax+a+2=0，当a为何值时，该方程：
（1）有两个不同的正根；
（2）有不同的两根且两根在（1，3）内．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网