题目内容
20.下列各图是正方体或正四面体,P,Q,R,S分别是所在棱的中点,这四个点中不共面的一个图是( )| A. |  | B. | 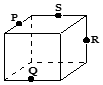 | C. | 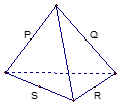 | D. |  |
分析 在A中,由PQ与SR相交,知P、Q、R、S四个点共面;在B中,由QR与PS相交,知P、Q、R、S四个点共面;在C中,由QR∥PA,知P、Q、R、S四个点共面;在D中,由QR和PS是异面直线,并且任意两个点的连线既不平行也不相交,知四个点共面不共面.
解答 解:在A中,由题意知在正方体中,PQ与SR相交,
则P、Q、R、S四个点共面,故A不对;
在B中,由题意知在正方体中,QR与PS相交,
所以P、Q、R、S四个点共面,故B不对;
在C中,因为PR和QS分别是相邻侧面的中位线,
所以PR∥BS,QS∥BD,即QR∥PA,所以P、Q、R、S四个点共面,故C不对;
在D中,根据图中几何体得,P、Q、R、S四个点中任意两个点都在两个平面内,
QR和PS是异面直线,并且任意两个点的连线既不平行也不相交,故四个点共面不共面,故D对;
故选:D.
点评 本题考查四点是否共面的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.设集合A={x|(x+1)(2-x)>0},集合B={x|1<x<3},则A∪B=( )
| A. | (-1,3) | B. | (-1,1) | C. | (1,2) | D. | (2,3) |
8.某高校《统计初步》课程的教师随机调查了选修该课的学生的一些情况,具体数据如表1:为了判断主修统计专业是否与性别有关,根据表中数据,得K2的观察值为k=$\frac{{50×{{(13×20-10×7)}^2}}}{23×27×20×30}$≈4.844,所以判断主修统计专业与性别有关,那么这种判断出错的可能性不超过( )
| 表1 | 非统计专业 | 统计专业 |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
| P(K2≥k0) | 0.05 | 0.025 | 0.01 | 0.005 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 |
| A. | 5% | B. | 2.5% | C. | 1% | D. | 0.5% |
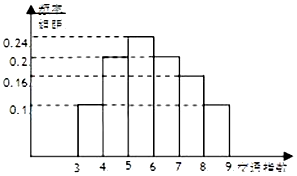 交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围为[0,10],分为五个级别,T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如右图.
交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围为[0,10],分为五个级别,T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如右图.