题目内容
17.函数$y=\sqrt{3}sinx+cosx$的图象可以由函数y=2sinx的图象至少向左平移$\frac{π}{6}$个单位得到.分析 令f(x)=2sinx,则f(x-φ)=2in(x-φ),依题意可得2sin(x-φ)=2sin(x+$\frac{π}{6}$),由-φ=2kπ-$\frac{π}{6}$(k∈Z),可得答案.
解答 解:∵$y=\sqrt{3}sinx+cosx$=2sin(x+$\frac{π}{6}$),
令f(x)=2sinx,
则f(x-φ)=2in(x-φ)(φ>0),
依题意可得2sin(x-φ)=2sin(x+$\frac{π}{6}$),
故-φ=2kπ-$\frac{π}{6}$(k∈Z),
即φ=-2kπ+$\frac{π}{6}$(k∈Z),
当k=0时,正数φmin=x+$\frac{π}{6}$,
故答案为:$\frac{π}{6}$.
点评 本题考查函数y=sinx的图象变换得到y=Asin(ωx+φ)(A>0,ω>0)的图象,得到-φ=2kπ-$\frac{π}{6}$(k∈Z)是关键,属于中档题.

练习册系列答案
相关题目
7.若一系列的函数解析式相同、值域相同,但定义域不同,则称这些函数为“同型异构”函数.那么函数解析式为y=-x2,x∈R,值域为{-1,-9}的“同型异构”函数有( )
| A. | 10个 | B. | 9个 | C. | 8个 | D. | 7个 |
8.某高校《统计初步》课程的教师随机调查了选修该课的学生的一些情况,具体数据如表1:为了判断主修统计专业是否与性别有关,根据表中数据,得K2的观察值为k=$\frac{{50×{{(13×20-10×7)}^2}}}{23×27×20×30}$≈4.844,所以判断主修统计专业与性别有关,那么这种判断出错的可能性不超过( )
| 表1 | 非统计专业 | 统计专业 |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
| P(K2≥k0) | 0.05 | 0.025 | 0.01 | 0.005 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 |
| A. | 5% | B. | 2.5% | C. | 1% | D. | 0.5% |
2.函数f(x)=aex-1-$\sqrt{x}$+1的图象在点(1,f(1))处的切线斜率为$\frac{5}{2}$,则实数a=( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 3 | D. | -3 |
6.若实数 x,y满足 (x-2)2+y2=1,则$\frac{y}{x}$的最大值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{3}$ |
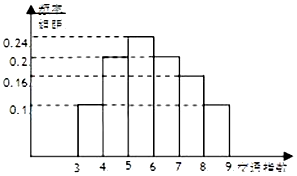 交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围为[0,10],分为五个级别,T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如右图.
交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围为[0,10],分为五个级别,T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如右图.