题目内容
用3米长的绳索围一个三角形,怎样围可以使这个三角形的面积最大?(限用导数法)
考点:利用导数求闭区间上函数的最值
专题:应用题,导数的综合应用
分析:可知当底边一定,另两边和是定值时,则这两边相等,即为等腰三角形时三角形面积最大,设底边长为x米,则另两边长为
米,
米,高为
=
米,面积S=
×
=
,两边平方后利用导数可求得最值.
| 3-x |
| 2 |
| 3-x |
| 2 |
(
|
| ||
| 2 |
| 1 |
| 2 |
x
| ||
| 2 |
x
| ||
| 4 |
解答:
解:当底边一定,另两边和是定值时,则这两边相等,即为等腰三角形时三角形面积最大,
∴设底边长为x米,则另两边长为
米,
米,高为
=
米,
面积S=
×
=
,
4S2=x2(9-6x)=-6x3+9x2,y′=-18x2+18x,
当0<x<1时y′>0,当x>1时,y′<0,
∴x=1时4S2取得极大值,也为最大值,4S2≤3,
S≤
,
∴当三角形是边长为1的等边三角形时,面积最大为
.
∴设底边长为x米,则另两边长为
| 3-x |
| 2 |
| 3-x |
| 2 |
(
|
| ||
| 2 |
面积S=
| 1 |
| 2 |
x
| ||
| 2 |
x
| ||
| 4 |
4S2=x2(9-6x)=-6x3+9x2,y′=-18x2+18x,
当0<x<1时y′>0,当x>1时,y′<0,
∴x=1时4S2取得极大值,也为最大值,4S2≤3,
S≤
| ||
| 2 |
∴当三角形是边长为1的等边三角形时,面积最大为
| ||
| 2 |
点评:该题考查利用导数研究函数的最值,在实际问题中正确建立函数模型是解题关键所在.

练习册系列答案
相关题目
下列四个命题中,真命题的是( )
| A、2是偶数且是无理数 |
| B、有些梯形内接于圆 |
| C、空间中的两个向量可能不共面 |
| D、?x∈R,x2-x-1≠0 |
某城市有3个演习点同时进行消防演习,现将4个消防队分配到这3个演习点,若每个演习点至少安排1个消防队,则不同的分配方案种数位( )
| A、12 | B、36 | C、72 | D、108 |
已知函数f(x)=2x2+bx+c(b,c∈R)的值域为[0,+∞),若关于x的不等式f(x)<m的解集为(n,n+10),则实数m的值为( )
| A、25 | B、-25 |
| C、50 | D、-50 |
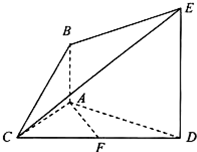 如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=4,DE=2AB=3,且F是CD的中点.
如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=4,DE=2AB=3,且F是CD的中点.