题目内容
在数列{an}中，已知a1=1，an+1=an+
，求{an}的通项公式．
| an |
| n+1 |
考点：归纳推理
专题：推理和证明
分析：由a1=1，an+1=an+
，求出a2、a3、a4、a5的值，由此归纳猜测{an}的通项公式an．
| an |
| n+1 |
解答：
解：数列{an}中，∵a1=1，an+1=an+
，
∴a2=a1+
=1+
=
，
a3=a2+
=
+
=2，
a4=a3+
=2+
=
，
a5=a4+
=
+
=3；
…，
猜测{an}的通项公式为an=
．
| an |
| n+1 |
∴a2=a1+
| a1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
a3=a2+
| a2 |
| 3 |
| 3 |
| 2 |
| ||
| 3 |
a4=a3+
| a3 |
| 4 |
| 2 |
| 4 |
| 5 |
| 2 |
a5=a4+
| a4 |
| 5 |
| 5 |
| 2 |
| ||
| 5 |
…，
猜测{an}的通项公式为an=
| n+1 |
| 2 |
点评：本题考查了数列的递推公式以及归纳推理的应用问题，解题时应根据递推公式计算出数列的前几项，由此归纳猜想{an}的通项公式，是基础题．
练习册系列答案
相关题目
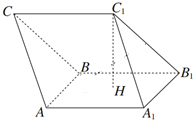如图所示，在三棱柱ABC-A1B1C1中，H是正方形AA1B1B的中心，AA1=2