题目内容
请画出函数y=1+丨x丨+
的图象，并求单调区间．
| x |
| 2 |
考点：函数的图象
专题：函数的性质及应用
分析：通过y=1+丨x丨+
=
．画出函数图象，利用数形结合求出单调区间．
| x |
| 2 |
|
解答：
解：y=1+丨x丨+
=
．画出函数图象，如图所示：
由图象可知函数的增区间[0，+∞），
函数的单调减区间：（-∞，0）．
解：y=1+丨x丨+| x |
| 2 |
|
由图象可知函数的增区间[0，+∞），
函数的单调减区间：（-∞，0）．
点评：本题主要考查带有绝对值的函数，函数的值域以及单调性，体现了数形结合的数学思想，属于中档题．
练习册系列答案
相关题目
已知y=f（x）=ln|x|，则下列各命题中，正确的命题是（ ）
A、x＞0时，f′（x）=
| ||||
B、无论x＞0，还是x＜0，都有f′（x）=
| ||||
C、x＞0时，f′（x）=
| ||||
| D、因为x=0时，f（x）无意义，所以对于y=ln|x|不能求导 |
已知集合A={y|y=log2x，x≥1}，B={x|y=
}，则A∩B=（ ）
| 1-x |
| A、[0，1] |
| B、（0，1） |
| C、[0，1） |
| D、（0，1] |
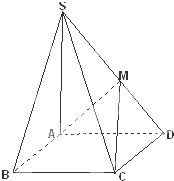如图，在四棱锥S-ABCD中，底面ABCD为矩形，SA⊥底面ABCD，M为SD的中点，且SA=AD=AB．