题目内容
已知点A、B的坐标分别是(0,-1)、(0,1),|AB|是|MA|和|MB|的等差中项
(1)求动点M的轨迹方程;
(2)设过(0,-2)的直线l与动点M的轨迹交于C、D两点,且
•
=2,求直线l的方程.
(1)求动点M的轨迹方程;
(2)设过(0,-2)的直线l与动点M的轨迹交于C、D两点,且
. |
| OC |
. |
| OD |
考点:直线与圆锥曲线的综合问题,轨迹方程
专题:圆锥曲线的定义、性质与方程
分析:(1)由等差数列的性质可得2|AB|=|MA|+|MB|=4,再利用椭圆的定义可知:动点M的轨迹是椭圆.
(2)点(0,-2)是椭圆的一个顶点,不妨取C(0,-2).设D(x0,y0),当直线l为y轴时,不满足
•
=2,应舍去.
设直线l的方程为y=kx-2,与椭圆的方程联立可得根与系数的关系,再利用数量积运算即可得出.
(2)点(0,-2)是椭圆的一个顶点,不妨取C(0,-2).设D(x0,y0),当直线l为y轴时,不满足
. |
| OC |
. |
| OD |
设直线l的方程为y=kx-2,与椭圆的方程联立可得根与系数的关系,再利用数量积运算即可得出.
解答:
解:(1)设M(x,y),
∵|AB|是|MA|和|MB|的等差中项,
∴2|AB|=|MA|+|MB|,
∴|MA|+|MB|=4>2=|AB|,
由椭圆的定义可知:动点M的轨迹是椭圆.
设椭圆的标准方程为:
+
=1(a>b>0).
∴a=2,c=1,b2=a2-c2=3.
∴动点M的轨迹方程为:
+
=1.
(2)∵点(0,-2)是椭圆的一个顶点,不妨取C(0,-2).
设D(x0,y0),当直线l为y轴时,不满足
•
=2,应舍去.
设直线l的方程为y=kx-2.
联立
,化为(3k2+4)x2-12kx=0,
解得x=0或
.∴D(
,
).
∵
•
=2,∴
=2,解得k=±
.
∴直线l的方程为:y=±
x-2.
∵|AB|是|MA|和|MB|的等差中项,
∴2|AB|=|MA|+|MB|,
∴|MA|+|MB|=4>2=|AB|,
由椭圆的定义可知:动点M的轨迹是椭圆.
设椭圆的标准方程为:
| y2 |
| a2 |
| x2 |
| b2 |
∴a=2,c=1,b2=a2-c2=3.
∴动点M的轨迹方程为:
| y2 |
| 4 |
| x2 |
| 3 |
(2)∵点(0,-2)是椭圆的一个顶点,不妨取C(0,-2).
设D(x0,y0),当直线l为y轴时,不满足
. |
| OC |
. |
| OD |
设直线l的方程为y=kx-2.
联立
|
解得x=0或
| 12k |
| 3k2+4 |
| 12k |
| 3k2+4 |
| 6k2-8 |
| 3k2+4 |
∵
. |
| OC |
. |
| OD |
| -2(6k2-8) |
| 3k2+4 |
| 2 |
| 3 |
∴直线l的方程为:y=±
| 2 |
| 3 |
点评:本题考查了等差数列的性质、椭圆的定义、直线与椭圆相交问题转化为方程联立得到根与系数的关系、数量积运算等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目

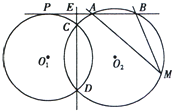 已知⊙O1和⊙O2交于点C和D,⊙O1上的点P处的切线交⊙O2于A、B点,交直线CD于点E,M是⊙O2上的一点,若PE=2,EA=1,∠AMB=30°,求⊙O2的半径.
已知⊙O1和⊙O2交于点C和D,⊙O1上的点P处的切线交⊙O2于A、B点,交直线CD于点E,M是⊙O2上的一点,若PE=2,EA=1,∠AMB=30°,求⊙O2的半径.