题目内容
(1)解不等式x2-4x+3>0;
(2)求值:
-
.
(2)求值:
| 1 |
| sin10° |
| ||
| cos10° |
考点:两角和与差的正弦函数,一元二次不等式的解法
专题:三角函数的求值,不等式的解法及应用
分析:(1)利用一元二次不等式的解法可求不等式x2-4x+3>0得解集;
(2)通分后,逆用两角差的正弦与二倍角的正弦即可求得答案.
(2)通分后,逆用两角差的正弦与二倍角的正弦即可求得答案.
解答:
解:(1)∵x2-4x+3=(x-3)(x-1)>0,
∴x>3或x<1,
∴原不等式的解集为{|x<1或x>3};
(2)
-
=
=
=
=4.
∴x>3或x<1,
∴原不等式的解集为{|x<1或x>3};
(2)
| 1 |
| sin10° |
| ||
| cos10° |
cos10°-
| ||
| sin10°cos10° |
2(
| ||||||
|
| 2sin(30°-10°) | ||
|
点评:本题考查一元二次不等式的解法与两角差的正弦与二倍角的正弦,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
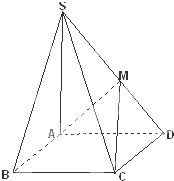 如图,在四棱锥S-ABCD中,底面ABCD为矩形,SA⊥底面ABCD,M为SD的中点,且SA=AD=AB.
如图,在四棱锥S-ABCD中,底面ABCD为矩形,SA⊥底面ABCD,M为SD的中点,且SA=AD=AB. 如图所示,已知正四棱柱ABCD-A1B1C1D1中,底面边长为2
如图所示,已知正四棱柱ABCD-A1B1C1D1中,底面边长为2