题目内容
4．已知奇函数f（x）在（0，+∞）上是增函数，且f（2）=0，则f（x）＞0的解集为（ ）| A． | （0，2） | B． | （-2，0） | C． | （-2，0）∪（2，+∞） | D． | （-2，2） |
分析 利用奇函数的对称性、单调性即可得出．
解答 
解：如图所示，
不等式f（x）＞0的解集为（-2，0）∪（2，+∞），
故选C．
点评 本题考查了奇函数的对称性、单调性，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
15．若集合{1，$\frac{b}{a}$，a}={0，a+b，a2}，则a2+b2=（ ）
| A． | -1 | B． | 1 | C． | 0 | D． | ±1 |
12．若A={x|x2-5x+4＜0}，B={x|x-2≤0}，则A∩B=（ ）
| A． | （0，1） | B． | （0，2] | C． | （1，2） | D． | （1，2] |
19．不等式x2+ax-b＜0的解集是（2，3），则bx2-ax-1＞0的解集是（ ）
| A． | $（\frac{1}{3}，\frac{1}{2}）$ | B． | $（\frac{1}{6}，1）$ | C． | $（-\frac{1}{2}，-\frac{1}{3}）$ | D． | $（-∞，-\frac{1}{2}）∪（-\frac{1}{3}，+∞）$ |
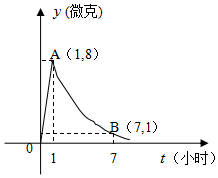某医药研究所开发一种新药，据监测，如果成人按规定的剂量服用，服用药后每毫升中的含药量y（微克）与服药的时间t（小时）之间近似满足如图所示的曲线，其中OA是线段，曲线AB是函数y=kat（t≥1，a＞0，且k，a是常数）的图象．
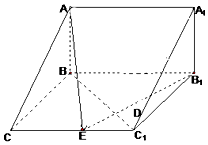如图，在三棱柱ABC-A1B1C1中，已知AB⊥侧面BB1C1C，CB⊥C1B，BC=1，CC1=2，A1B1=$\sqrt{2}$，