题目内容
4．
如图所示，在△ABC中，M是BC的中点，AN平分∠BAC，BN⊥AN，若AB=14，AC=19，则MN的长为（ ）| A． | 2 | B． | 2.5 | C． | 3 | D． | 3.5 |
分析 延长BN交AC于D，运用三角形全等的判定和性质，可得N为BD的中点，MN是△BCD的中位线，由中位线定理，计算即可得到所求值．
解答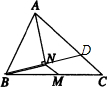 
解：延长BN交AC于D，
∵∠BAN=∠DAN，AN=AN，∠ANB=∠AND，
∴△ABN≌△ADN，N为BD的中点，
∴MN是△BCD的中位线，
∴MN=$\frac{1}{2}$CD=$\frac{1}{2}$（AC-AD）=$\frac{1}{2}$（AC-AB），
∵AB=14，AC=19，
∴MN=$\frac{1}{2}$（19-14）=2.5．
故选：B．
点评 本题考查三角形的全等的判定和性质，以及中位线定理的运用，考查运算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
15．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线平行于直线l：3x-2y+3$\sqrt{13}$=0，且双曲线的一个焦点在直线l上，则双曲线方程为（ ）
| A． | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 | B． | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 | C． | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1 | D． | $\frac{5{x}^{2}}{16}$-$\frac{5{y}^{2}}{9}$=1 |
12．函数f（x）=2-$\frac{3}{x}$在区间[1，3]上的最大值是（ ）
| A． | 2 | B． | 3 | C． | -1 | D． | 1 |
19．下列说法中错误的是（ ）
| A． | 垂直于同一条直线的两条直线相互垂直 | |
| B． | 若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行 | |
| C． | 若一个平面经过另一个平面的垂线，那么这两个平面相互垂直 | |
| D． | 若一个平面内的两条相交直线与另一个平面内的相交直线分别平行，那么这两个平面相互平行 |
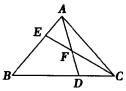如图，在△ABC中，AE：EB=1：3，BD：DC=2：1，AD与CE相交于点F，则$\frac{EF}{FC}+\frac{AF}{FD}$的值为$\frac{3}{2}$．