Question

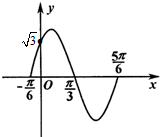函数f（x）=Asin（ωx+φ），（A＞0，ω＞0，0＜φ＜

π

2

）的图象如图所示．
（1）求函数f（x）的解析式；
（2）已知0＜α＜

π

2

且f（

α

2

）=

6

5

，求sinα的值．

Answer 1

考点：函数y=Asin（ωx+φ）的图象变换

专题：三角函数的图像与性质

分析：（1）根据图象确定A，ω 和φ的值，即可求函数f（x）的解析式；
（2）根据条件0＜α＜

π

2

且f（

α

2

）=

6

5

，利用两角和差的正弦公式即可求sinα的值．

解答： 解：（1）函数的周期T=

5π

6

-(-

π

6

)=π，即ω=

2π

T

=

2π

π

=2，
∵f（-

π

6

）=Asin（-

π

3

+φ）=0，∴-

π

3

+φ=kπ，
又∵0＜φ＜

π

2

，∴当k=0时，φ=

π

3

，
则f（x）=Asin（2x+

π

3

），
∵f（0）=Asin

π

3

3 A

2

=

3

，
∴A=2，
∴f（x）=2sin（2x+

π

3

）．
（2）∵f（

α

2

）=2sin（α+

π

3

）=

6

5

，
∴sin（α+

π

3

）=

3

5

，cos（α+

π

3

）=±

4

5

，
∴sinα=sin[（α+

π

3

）-

π

3

]=sin（α+

π

3

）cos

π

3

-cos（α+

π

3

）sin

π

3

=

3

10

±

4 3

10

，
又∵0＜α＜

π

2

，
∴sinα＞0，
∴sinα=

3

10

+

4 3

10

=

3+4 3

10

．

点评：本题考查的知识点是由函数y=Asin（ωx+ϕ）的部分图象确定其解析式，根据A，ω，φ的关系是解决本题的关键．