题目内容
设点D，E分别在△ABC的边BC，AC上，线段AD，BE相交于点F，则“F为△ABC的重心”是“
=
=2”的（ ）
| AF |
| FD |
| BF |
| FE |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：若F为△ABC的重心，则
=
=2．反之也成立，连接DE，由于
=
=2，∠AFB=∠DFE．可得△AFB∽△DFE，
=
，DE∥AB，于是
=
，因此点D是线段BC的中点，可得点F是△ABC的重心．即可得出．
| AF |
| FD |
| BF |
| FE |
| AF |
| FD |
| BF |
| FE |
| DE |
| AB |
| 1 |
| 2 |
| CD |
| CB |
| 1 |
| 2 |
解答：
解：若F为△ABC的重心，则
=
=2．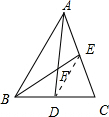
反之也成立，连接DE，∵
=
=2，∠AFB=∠DFE．
∴△AFB∽△DFE，
∴∠ADE=∠BAF，
=
．
∴DE∥AB，
∴
=
，
∴点D是线段BC的中点，
∴点F是△ABC的重心．
∴“F为△ABC的重心”是“
=
=2”的充要条件．
故选：C．
| AF |
| FD |
| BF |
| FE |
反之也成立，连接DE，∵
| AF |
| FD |
| BF |
| FE |
∴△AFB∽△DFE，
∴∠ADE=∠BAF，
| DE |
| AB |
| 1 |
| 2 |
∴DE∥AB，
∴
| CD |
| CB |
| 1 |
| 2 |
∴点D是线段BC的中点，
∴点F是△ABC的重心．
∴“F为△ABC的重心”是“
| AF |
| FD |
| BF |
| FE |
故选：C．
点评：本题考查了三角形重心的性质、平行线分线段成比例定理、相似三角形的判定与性质定理、充要条件的判定，考查了推理能力，属于中档题．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
一个三角形用斜二测画法所作的直观图是一个边长为1正三角形，则原三角形的面积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图1，⊙O的直径AB=4，点C，D为⊙O上任意两点，∠CAB=45°，∠DAB=60°，F为
已知P是椭圆
+y2=1上第一象限内的点，A（2，0），B（0，1），O为原点，则四边形OAPB面积的最大值为（ ）
| x2 |
| 4 |
| A、2 | ||
B、
| ||
C、
| ||
| D、1 |