Question

下列命题中，是假命题的有

 

（写出所有假命题的序号）
①在等比数列（-∞，5]中，若a₁=9，a₅=1，则a₃的值是±3；
②把函数y=sin(2x+

π

3

)的图象向右平移

π

3

个单位得到y=sin2x的图象；
③点(

π

8

，0)为函数f(x)=tan(2x+

π

4

)图象的一个对称中心；
④若|

a

|=1，|

b

|=2，向量

a

与向量

b

的夹角为120°，则

b

在向量

a

上的投影为1；
⑤函数f（x）=ln|x-1|+

1

x

有两个零点．

Answer 1

考点：命题的真假判断与应用

专题：简易逻辑

分析：由等比数列的性质判断①错误；直接由三角函数的图象平移说明②错误；根据

π

2

的正切值不存在结合正切函数的图象说明③正确；
求出

b

在向量

a

上的投影说明④错误；画图求得函数f（x）=ln|x-1|+

1

x

的零点说明⑤错误．

解答： 解：对于①，在等比数列{a_n}中，若a₁=9，a₅=1，则a₃的值是3，若a₃=-3，则a22＜0，命题①错误；
对于②，把函数y=sin(2x+

π

3

)的图象向右平移

π

3

个单位得到y=sin[2(x-

π

3

)+

π

3

]=sin(2x-

π

3

)的图象，命题②错误；
对于③，∵2×

π

8

+

π

4

=

π

2

，其正切值不存在，
∴点(

π

8

，0)为函数f(x)=tan(2x+

π

4

)图象的一个对称中心，命题③正确；
对于④，若|

a

|=1，|

b

|=2，向量

a

与向量

b

的夹角为120°，则

b

在向量

a

上的投影为|

b

|cos120°=2×(-

1

2

)=-1，命题④错误；
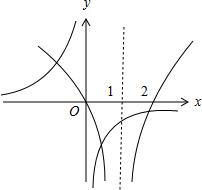
对于⑤，函数f（x）=ln|x-1|+

1

x

的零点即为方程ln|x-1|=

1

x

的根，也就是函数y=ln|x-1|与y=

1

x

的交点的横坐标，
如图，由图可知，函数f（x）=ln|x-1|+

1

x

有三个零点，命题⑤错误．
．
故答案为：①②④⑤．

点评：本题考查了命题的真假判断与应用，考查了三角函数的图象和性质，考查了函数零点的判断，是中档题．