题目内容
18.某函数部分图象如图所示,它的函数解析式可能是( )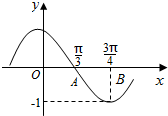
| A. | $y=sin(-\frac{5}{6}x+\frac{3π}{5})$ | B. | $y=sin(\frac{6}{5}x-\frac{2π}{5})$ | C. | $y=sin(\frac{6}{5}x+\frac{3π}{5})$ | D. | $y=-cos(\frac{5}{6}x+\frac{3π}{5})$ |
分析 根据已知函数的图象,可分析出函数的最值,确定A的值,分析出函数的周期,确定ω的值,将($\frac{π}{3}$,0)代入解析式,可求出φ值,进而求出函数的解析式.
解答 解:不妨令该函数解析式为y=Asin(ωx+ϕ),由图知A=1,$\frac{T}{4}=\frac{3π}{4}-\frac{π}{3}$=$\frac{5π}{12}$,
于是$\frac{2π}{ω}=\frac{5π}{3}$,即$ω=\frac{6}{5}$,
因$\frac{π}{3}$是函数减时经过的零点,
于是$\frac{6}{5}•\frac{π}{3}+ϕ=2kπ+π$,k∈Z,
所以ϕ可以是$\frac{3π}{5}$,
故选:C.
点评 本题考查的知识点是正弦型函数解析式的求法,其中关键是要根据图象分析出函数的最值,周期等,进而求出A,ω和φ值,属于基本知识的考查.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
19.下列四组函数中,有相同图象的一组是( )
| A. | f(x)=x,g(x)=$\sqrt{{x}^{2}}$ | B. | f(x)=x,g(x)=$\root{3}{{x}^{3}}$ | ||
| C. | f(x)=cosx,g(x)=sin($\frac{3π}{2}$+x) | D. | f(x)=lnx2,g(x)=2lnx |
6.某厂采用新技术改造后生产甲产品的产量x(吨)与相应的生产成本y(万元)的几组对照数据.
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(3)已知该厂技改前生产50吨甲产品的生产成本为40万元.试根据(2)求出的线性回归方程,预测生产50吨甲产品的生产成本比技改前降低多少万元?
(参考数据:$\sum_{i=1}^4{x_i^2=86}$$\sum_{i=1}^4{y_i^2=66}$.5$\sum_{i=1}^4{{x_i}{y_i}=75}$.5,$\widehat{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$)
| x | 3 | 4 | 5 | 6 |
| y | 3 | 3.5 | 4.5 | 5 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(3)已知该厂技改前生产50吨甲产品的生产成本为40万元.试根据(2)求出的线性回归方程,预测生产50吨甲产品的生产成本比技改前降低多少万元?
(参考数据:$\sum_{i=1}^4{x_i^2=86}$$\sum_{i=1}^4{y_i^2=66}$.5$\sum_{i=1}^4{{x_i}{y_i}=75}$.5,$\widehat{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$)
10.设全集U={1,2,3,4,5},集合 M={2,4},集合 N={3,5},则(∁UM)∩N=( )
| A. | {1,5} | B. | {3,5} | C. | {1,3,5} | D. | {2,4,5} |
7.二项式(x+$\frac{1}{x^2}$)6的展开式中,常数项为( )
| A. | 64 | B. | 30 | C. | 15 | D. | 1 |
8.某大学志愿者协会有10名同学,成员构成如下表,其中表中部分数据不清楚,只知道从这10名同学中随机抽取一位,抽到该名同学为“数学专业”的概率为$\frac{2}{5}$.
(1)求m,n的值;
(2)现从男同学中随机选取2名同学,进行社会公益活动(每位同学被选到的可能性相同),求选出的这2名男同学中至少有一位同学是“数学专业”的概率.
| 专业 性别 | 中文 | 英语 | 数学 | 体育 |
| 男 | n | 1 | m | 1 |
| 女 | 1 | 1 | 1 | 1 |
(2)现从男同学中随机选取2名同学,进行社会公益活动(每位同学被选到的可能性相同),求选出的这2名男同学中至少有一位同学是“数学专业”的概率.