题目内容
6.某厂采用新技术改造后生产甲产品的产量x(吨)与相应的生产成本y(万元)的几组对照数据.| x | 3 | 4 | 5 | 6 |
| y | 3 | 3.5 | 4.5 | 5 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(3)已知该厂技改前生产50吨甲产品的生产成本为40万元.试根据(2)求出的线性回归方程,预测生产50吨甲产品的生产成本比技改前降低多少万元?
(参考数据:$\sum_{i=1}^4{x_i^2=86}$$\sum_{i=1}^4{y_i^2=66}$.5$\sum_{i=1}^4{{x_i}{y_i}=75}$.5,$\widehat{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$)
分析 (1)把所给的四对数据写成对应的点的坐标,在坐标系中描出来,得到散点图.
(2)根据所给的这组数据求出利用最小二乘法所需要的几个数据,代入求系数b的公式,求得结果,再把样本中心点代入,求出a的值,得到线性回归方程.
(3)根据上一问所求的线性回归方程,把x=50代入线性回归方程,即可预测生产50吨甲产品的生产成本比技改前降低多少.
解答  解:(1)把所给的四对数据写成对应的点的坐标,在坐标系中描出来,得到散点图 …(2分)
解:(1)把所给的四对数据写成对应的点的坐标,在坐标系中描出来,得到散点图 …(2分)
(2)由已知$\sum_{i=1}^4{x_i^2=86}$,$\sum_{i=1}^4{y_i^2=66}.5$,$\sum_{i=1}^4{{x_i}{y_i}=75}.5$,$\overline x=4.5$,$\overline y=4$,
所以,由最小二乘法确定的回归方程的系数为:
$\widehat{b}$=$\frac{75.5-4×4×4.5}{{86-4×{{4.5}^2}}}=0.7$…(5分)
$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=4-0.7×4.5=0.85 …(7分)
因此,所求的线性回归方程为$\widehat{y}$=0.7x+0.85 …(8分)
(3)由(2)的回归方程及技改前生产50吨甲产品的生产成本,得降低的生产成本为:
40-(0.7×50+0.85)=4.15(万元). …(12分)
点评 本题考查线性回归方程,两个变量之间的关系,除了函数关系,还存在相关关系,通过建立回归直线方程,就可以根据其部分观测值,获得对这两个变量之间整体关系的了解.

| A. | 5,2 | B. | 16,2 | C. | 16,18 | D. | 16,9 |
| A. | (0,4] | B. | [0,4] | C. | (-∞,0)∪[4,+∞) | D. | (-∞,0)∪(4,+∞) |
| A. | 2x-8 | B. | 8-2x | C. | 10 | D. | -10 |
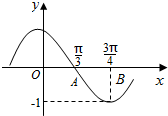
| A. | $y=sin(-\frac{5}{6}x+\frac{3π}{5})$ | B. | $y=sin(\frac{6}{5}x-\frac{2π}{5})$ | C. | $y=sin(\frac{6}{5}x+\frac{3π}{5})$ | D. | $y=-cos(\frac{5}{6}x+\frac{3π}{5})$ |

| A. | 36 | B. | 18 | C. | 12 | D. | 6 |