题目内容
3.log2$\sqrt{\frac{7}{72}}$+log26-$\frac{1}{2}$log228=$-\frac{3}{2}$;0.0081${\;}^{\frac{1}{4}}$-($\frac{27}{8}$)${\;}^{-\frac{2}{3}}$+$\sqrt{3}$•$\root{3}{\frac{3}{2}}$•$\root{6}{12}$=$\frac{257}{90}$.分析 利用对数、指数的性质、运算法则求解.
解答 解:log2$\sqrt{\frac{7}{72}}$+log26-$\frac{1}{2}$log228
=$lo{g}_{2}(\sqrt{\frac{7}{72}}×6÷\sqrt{28})$
=$lo{g}_{2}(\frac{1}{12\sqrt{2}}×6)$
=$lo{g}_{2}\frac{1}{2\sqrt{2}}$
=-$\frac{3}{2}$.
0.0081${\;}^{\frac{1}{4}}$-($\frac{27}{8}$)${\;}^{-\frac{2}{3}}$+$\sqrt{3}$•$\root{3}{\frac{3}{2}}$•$\root{6}{12}$
=[(0.3)4]${\;}^{\frac{1}{4}}$-[($\frac{3}{2}$)3]${\;}^{-\frac{2}{3}}$+${3}^{\frac{1}{2}}•\frac{{3}^{\frac{1}{3}}}{{2}^{\frac{1}{3}}}•{3}^{\frac{1}{6}}•{2}^{\frac{1}{3}}$
=0.3-$\frac{4}{9}$+3
=$\frac{257}{90}$.
故答案为:$-\frac{3}{2},\frac{257}{90}$.
点评 本题考查对数式、指数式化简求值,是基础题,解题时要认真审题,注意对数、指数的性质、运算法则的合理运用.

练习册系列答案
相关题目
14.若数据x1,x2,x3,…,xn的平均数为$\overline{x}$=5,方差σ2=2,则数据3x1+1,3x2+1,3x3+1,…,3xn+1的平均数和方差分别为( )
| A. | 5,2 | B. | 16,2 | C. | 16,18 | D. | 16,9 |
11.若实数x满足log2x=2+cosθ,则|x+1|+|x-9|的值等于( )
| A. | 2x-8 | B. | 8-2x | C. | 10 | D. | -10 |
18.某函数部分图象如图所示,它的函数解析式可能是( )
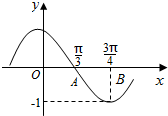

| A. | $y=sin(-\frac{5}{6}x+\frac{3π}{5})$ | B. | $y=sin(\frac{6}{5}x-\frac{2π}{5})$ | C. | $y=sin(\frac{6}{5}x+\frac{3π}{5})$ | D. | $y=-cos(\frac{5}{6}x+\frac{3π}{5})$ |
15.某三棱锥的三视图如图所示,则该三棱锥的体积是( )


| A. | 36 | B. | 18 | C. | 12 | D. | 6 |
12.在数列{an}中,a1=1,an+1=2an,Sn为{an}的前n项和,则S5=( )
| A. | -30 | B. | 31 | C. | -32 | D. | 33 |
13.设p:y=cx是R上的单调递减函数;q:函数g(x)=lg(2cx2+2x+1)的值域为R.如果“p且q”为假命题,“p或q”为真命题,则正实数c的取值范围是( )
| A. | $({\frac{1}{2},1})$ | B. | $({\frac{1}{2},+∞})$ | C. | $({0,\frac{1}{2}}]∪[{1,+∞})$ | D. | $({0,\frac{1}{2}})$ |