题目内容
8.某大学志愿者协会有10名同学,成员构成如下表,其中表中部分数据不清楚,只知道从这10名同学中随机抽取一位,抽到该名同学为“数学专业”的概率为$\frac{2}{5}$.| 专业 性别 | 中文 | 英语 | 数学 | 体育 |
| 男 | n | 1 | m | 1 |
| 女 | 1 | 1 | 1 | 1 |
(2)现从男同学中随机选取2名同学,进行社会公益活动(每位同学被选到的可能性相同),求选出的这2名男同学中至少有一位同学是“数学专业”的概率.
分析 (1)设事件A:从10位学生中随机抽取一位,抽到该名同学为“数学专业”.由题意可知,“数学专业”的学生共有(1+m)人.由此利用抽到该名同学为“数学专业”的概率为$\frac{2}{5}$,能求出m,n的值.
(2)由题意可知,男生共有6人,分别记为a1,a2,a3,a4,a5,a6.其中数学专业的男生为a4,a5,a6.从中任意抽取2位,利用列举法能求出至少有一位同学是“数学专业”的概率.
解答 解:(1)设事件A:从10位学生中随机抽取一位,抽到该名同学为“数学专业”.
由题意可知,“数学专业”的学生共有(1+m)人.
则$P(A)=\frac{1+m}{10}=\frac{2}{5}$.解得 m=3.
所以n=1. …(6分)
(2)由题意可知,男生共有6人,分别记为a1,a2,a3,a4,a5,a6.其中数学专业的男生为a4,a5,a6.
从中任意抽取2位,可表示为:
a1a2,a1a3,a1a4,a1a5,a1a6,a2a3,a2a4,a2a5,a2a6,a3a4,a3a5,a3a6,a4a5,a4a6,a5a6,共15种可能.
设事件B:选出的这2名男同学中至少有一位同学是“数学专业”.
事件B包括:a1a4,a1a5,a1a6,a2a4,a2a5,a2a6,a3a4,a3a5,a3a6,a4a5,a4a6,a5a6,共12种可能.
所以至少有一位同学是“数学专业”的概率是$P(B)=\frac{12}{15}=\frac{4}{5}$. …(12分)
点评 本题考查实数值的求法,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
18.某函数部分图象如图所示,它的函数解析式可能是( )
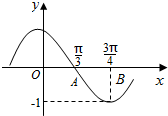

| A. | $y=sin(-\frac{5}{6}x+\frac{3π}{5})$ | B. | $y=sin(\frac{6}{5}x-\frac{2π}{5})$ | C. | $y=sin(\frac{6}{5}x+\frac{3π}{5})$ | D. | $y=-cos(\frac{5}{6}x+\frac{3π}{5})$ |
13.设p:y=cx是R上的单调递减函数;q:函数g(x)=lg(2cx2+2x+1)的值域为R.如果“p且q”为假命题,“p或q”为真命题,则正实数c的取值范围是( )
| A. | $({\frac{1}{2},1})$ | B. | $({\frac{1}{2},+∞})$ | C. | $({0,\frac{1}{2}}]∪[{1,+∞})$ | D. | $({0,\frac{1}{2}})$ |
17.下列叙述中正确的是( )
| A. | “m=2”是“l1:2x+(m+1)y+4=0与l2:mx+3y-2=0平行”的充分条件 | |
| B. | “方程Ax2+By2=1表示椭圆”的充要条件是“A≠B” | |
| C. | 命题“?x∈R,x2≥0”的否定是“?x0∈R,x02≥0” | |
| D. | 命题“a、b都是偶数,则a+b是偶数”的逆否命题为“a+b不是偶数,则a、b都是奇数” |
18.在下列关于函数f(x)=$\frac{1}{2}$cosx+$\frac{1}{2}$|cosx|说法中,正确的是( )
| A. | 最小正周期为π | B. | 值域为[0,1] | ||
| C. | 在[$\frac{π}{2}$,$\frac{3π}{2}$]上单调递减 | D. | (π,0)是其图象的一个对称中心 |
