题目内容
7.二项式(x+$\frac{1}{x^2}$)6的展开式中,常数项为( )| A. | 64 | B. | 30 | C. | 15 | D. | 1 |
分析 在二项展开式的通项公式中,令x的幂指数等于0,求出r的值,再求得常数项.
解答 解:二项式(x+$\frac{1}{x^2}$)6的展开式的通项公式为
Tr+1=${C}_{6}^{r}$•x6-r•($\frac{1}{{x}^{2}}$)r=${C}_{6}^{r}$•x6-3r,
令6-3r=0,求得r=2,
故展开式中的常数项为${C}_{6}^{2}$=15,
故选:C.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,是基础题目.

练习册系列答案
相关题目
18.某函数部分图象如图所示,它的函数解析式可能是( )
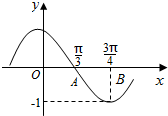

| A. | $y=sin(-\frac{5}{6}x+\frac{3π}{5})$ | B. | $y=sin(\frac{6}{5}x-\frac{2π}{5})$ | C. | $y=sin(\frac{6}{5}x+\frac{3π}{5})$ | D. | $y=-cos(\frac{5}{6}x+\frac{3π}{5})$ |
15.某三棱锥的三视图如图所示,则该三棱锥的体积是( )


| A. | 36 | B. | 18 | C. | 12 | D. | 6 |
2.复数z=1-i,则$\overrightarrow{z}$对应的点所在的象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
12.在数列{an}中,a1=1,an+1=2an,Sn为{an}的前n项和,则S5=( )
| A. | -30 | B. | 31 | C. | -32 | D. | 33 |
17.下列叙述中正确的是( )
| A. | “m=2”是“l1:2x+(m+1)y+4=0与l2:mx+3y-2=0平行”的充分条件 | |
| B. | “方程Ax2+By2=1表示椭圆”的充要条件是“A≠B” | |
| C. | 命题“?x∈R,x2≥0”的否定是“?x0∈R,x02≥0” | |
| D. | 命题“a、b都是偶数,则a+b是偶数”的逆否命题为“a+b不是偶数,则a、b都是奇数” |