题目内容
19.下列四组函数中,有相同图象的一组是( )| A. | f(x)=x,g(x)=$\sqrt{{x}^{2}}$ | B. | f(x)=x,g(x)=$\root{3}{{x}^{3}}$ | ||
| C. | f(x)=cosx,g(x)=sin($\frac{3π}{2}$+x) | D. | f(x)=lnx2,g(x)=2lnx |
分析 根据两个函数的定义域相同,对应法则也相同,即可判断它们是同一函数,对应的图象也相同.
解答 解:对于A,f(x)=x(x∈R),与g(x)=$\sqrt{{x}^{2}}$=|x|(x∈R)的对应法则不同,不是相同函数,函数图象不同;
对于B,f(x)=x(x∈R),与g(x)=$\root{3}{{x}^{3}}$=x(x∈R)的定义域相同,对应法则也相同,是相同函数,函数图象也相同;
对于C,f(x)=cosx(x∈R),与g(x)=sin($\frac{3π}{2}$+x)=-cosx(x∈R)的对应法则不同,不是相同函数,函数图象不同;
对于D,f(x)=lnx2=2ln|x|的定义域为{x|x≠0},g(x)=2lnx的定义域为{x|x>0},两个函数的定义域不同,不是相同函数,函数图象也不同.
故选:B.
点评 本题考查了判断两个函数是否为同一函数的应用问题,判断的标准是看两个函数的定义域和对应法则是否相同,是基础题目.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
11.log34•log48•log87•log7m=log39,那么m=( )
| A. | 27 | B. | 18 | C. | 9 | D. | $\frac{9}{2}$ |
18.某函数部分图象如图所示,它的函数解析式可能是( )
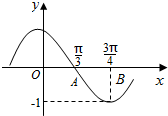

| A. | $y=sin(-\frac{5}{6}x+\frac{3π}{5})$ | B. | $y=sin(\frac{6}{5}x-\frac{2π}{5})$ | C. | $y=sin(\frac{6}{5}x+\frac{3π}{5})$ | D. | $y=-cos(\frac{5}{6}x+\frac{3π}{5})$ |