题目内容
13.若α,$β∈(\frac{π}{2},\;\;π)$,且sin(α-β)=$\frac{5}{13}$,sinβ=$\frac{4}{5}$,求sinα=$\frac{33}{65}$.分析 由条件利用同角三角函数的基本关系求得cosβ、cos(α-β)的值,再利用两角差的正弦公式求得sinα=sin[(α-β)+β]的值.
解答 解:若α,$β∈(\frac{π}{2},\;\;π)$,且sin(α-β)=$\frac{5}{13}$,sinβ=$\frac{4}{5}$,∴α-β为锐角,cosβ=-$\sqrt{{1-sin}^{2}β}$=-$\frac{3}{5}$,
∴cos(α-β)=$\sqrt{{1-sin}^{2}(α-β)}$=$\frac{12}{13}$,
∴sinα=sin[(α-β)+β]=sin(α-β)cosβ+cos(α-β)sinβ=$\frac{5}{13}$•(-$\frac{3}{5}$)+$\frac{12}{13}$•$\frac{4}{5}$=$\frac{33}{65}$,
故答案为:$\frac{33}{65}$.
点评 本题主要考查同角三角函数的基本关系,两角差的正弦公式的应用,属于基础题.

练习册系列答案
相关题目
4.若直线l:xsinθ+2ycosθ=1与圆C:x2+y2=1相切,则直线l的方程为( )
| A. | x=1 | B. | x=±1 | C. | y=1 | D. | y=±1 |
1.命题p:?x∈R,ax2+ax+1>0,若?p是真命题,则实数a的取值范围是( )
| A. | (0,4] | B. | [0,4] | C. | (-∞,0)∪[4,+∞) | D. | (-∞,0)∪(4,+∞) |
18.某函数部分图象如图所示,它的函数解析式可能是( )
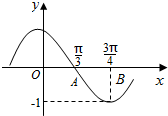

| A. | $y=sin(-\frac{5}{6}x+\frac{3π}{5})$ | B. | $y=sin(\frac{6}{5}x-\frac{2π}{5})$ | C. | $y=sin(\frac{6}{5}x+\frac{3π}{5})$ | D. | $y=-cos(\frac{5}{6}x+\frac{3π}{5})$ |
2.复数z=1-i,则$\overrightarrow{z}$对应的点所在的象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
