题目内容
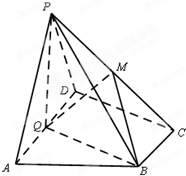如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC上的点，PA=PD=2，BC=| 1 |
| 2 |
| 3 |
（1）求证：平面PQB⊥平面PAD；
（2）设PM=2MC，求二面角M-BQ-C的余弦．
考点：异面直线及其所成的角,平面与平面垂直的判定
专题：空间位置关系与距离,空间角
分析：（1）由于BC∥AD，BC=
AD，Q为AD的中点，可判定四边形BCDQ为平行四边形，于是QB∥CD．已知CD⊥AD，可得BQ⊥AD．由于平面PAD⊥底面ABCD，平面PAD∩底面ABCD
=AD，利用线面垂直的性质定理可得：平面PQB⊥平面PAD；
（2）建立如图所示的空间直角坐标系，利用二面角的两个半平面的法向量的夹角即可得出．
| 1 |
| 2 |
=AD，利用线面垂直的性质定理可得：平面PQB⊥平面PAD；
（2）建立如图所示的空间直角坐标系，利用二面角的两个半平面的法向量的夹角即可得出．
解答：
（1）证明：∵BC∥AD，BC=
AD，Q为AD的中点，
∴BC
QD，
∴四边形BCDQ为平行四边形，
∴QB∥CD．
∵CD⊥AD，
∴BQ⊥AD．
∵平面PAD⊥底面ABCD，平面PAD∩底面ABCD=AD，
∴平面PQB⊥平面PAD；
（2）解：建立如图所示的空间直角坐标系，
则Q（0，0，0），B(0，
，0)，C(-1，
，0)，D（-1，0，0），P(0，0，
)．
∵
=2
，∴
-
=2(
-
)，∴3
=2
+
=2(-1，
，0)+(0，0，
)=(-2，2
，
)，
∴
=(-
，
，
)，即M(-
，
，
)．
设平面BMQ的法向量为
=（x，y，z），则
，取x=
，则y=0，z=2．
∴
=(
，0，2)．
取平面BCDQ的法向量
=（0，0，1）．
∴cos＜
，
＞=
=
=
．
∴二面角M-BQ-C的余弦为
．
| 1 |
| 2 |
∴BC
| ∥ |
. |
∴四边形BCDQ为平行四边形，
∴QB∥CD．
∵CD⊥AD，
∴BQ⊥AD．
∵平面PAD⊥底面ABCD，平面PAD∩底面ABCD=AD，
∴平面PQB⊥平面PAD；
（2）解：建立如图所示的空间直角坐标系，
则Q（0，0，0），B(0，
| 3 |
| 3 |
| 3 |
∵
| PM |
| MC |
| QM |
| QP |
| QC |
| QM |
| QM |
| QC |
| QP |
| 3 |
| 3 |
| 3 |
| 3 |
∴
| QM |
| 2 |
| 3 |
2
| ||
| 3 |
| ||
| 3 |
| 2 |
| 3 |
2
| ||
| 3 |
| ||
| 3 |
设平面BMQ的法向量为
| m |
|
| 3 |
∴
| m |
| 3 |
取平面BCDQ的法向量
| n |
∴cos＜
| m |
| n |
| ||||
|
|
| 2 | ||
|
2
| ||
| 7 |
∴二面角M-BQ-C的余弦为
2
| ||
| 7 |
点评：本题考查了平行四边形的判定与性质定理、线面垂直的性质、建立空间直角坐标系利用二面角的两个半平面的法向量的夹角求异面直线所成的角等基础知识与基本技能方法，考查了推理能力和计算能力，属于难题．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
已知直线l的方程为
x-y+
=0，则它的倾斜角为（ ）
| 3 |
| ||
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，梯形BCDE中，DE∥BC，CD⊥DE，ED=DC=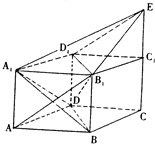
如图，已知直四棱柱ABCD-A1B1C1D1中，AB=AA1，底面ABCD为菱形，∠ADC=120°，E为CC1延长线上一点．