题目内容
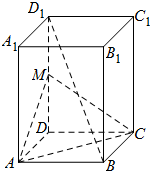 已知正四棱柱ABCD-A1B1C1D1中,M是DD1的中点.
已知正四棱柱ABCD-A1B1C1D1中,M是DD1的中点.(Ⅰ)求证:BD1∥平面AMC;
(Ⅱ)求证:AC⊥BD1;
(Ⅲ)在线段BB1上是否存在点P,当
| BP |
| BB1 |
考点:平面与平面平行的性质,空间中直线与直线之间的位置关系,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)连结BD交AC于N,连结MN.由此利用三角形中位线定理能证明BD1∥平面AMC.
(Ⅱ)由正方形性质得AC⊥BD,由线面垂直得DD1⊥AC,由此能证明AC⊥BD1.
(Ⅲ)当λ=
,平面A1PC1∥平面AMC.由已知条件推导出四边形ABQM是平行四边形,从而能证明平面A1PC1∥平面AMC.
(Ⅱ)由正方形性质得AC⊥BD,由线面垂直得DD1⊥AC,由此能证明AC⊥BD1.
(Ⅲ)当λ=
| 1 |
| 2 |
解答:
(本小题满分14分)
(Ⅰ)证明:在正四棱柱ABCD-A1B1C1D1中,连结BD交AC于N,连结MN.
因为ABCD为正方形,所以N为BD中点.…(1分)
在△DBD1中,因为M为DD1中点,
所以BD1∥MN.…(2分)
因为MN?平面AMC,BD1不包含于平面AMC,…(4分)
所以BD1∥平面AMC.…(5分)
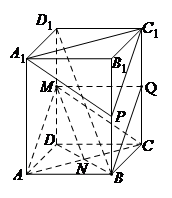 (Ⅱ)证明因为ABCD为正方形,
(Ⅱ)证明因为ABCD为正方形,
所以AC⊥BD.…(6分)
因为DD1⊥平面ABCD,
所以DD1⊥AC.…(7分)
因为DD1∩BD=D,…(8分)
所以AC⊥平面BDD1.…(9分)
因为BD1?平面BDD1,
所以AC⊥BD1.…(10分)
(Ⅲ)解:当λ=
,即点P为线段BB1的中点时,平面A1PC1∥平面AMC.…(11分)
因为AA1∥CC1,且AA1=CC1,
所以四边形AA1C1C是平行四边形.
所以AC∥A1C1.…(12分)
取CC1的中点Q,连结MQ,QB.
因为M为DD1中点,
所以MQ∥AB,且MQ=AB,
所以四边形ABQM是平行四边形.
所以BQ∥AM.…(13分)
同理BQ∥C1P.
所以AM∥C1P.
因为A1C1∩C1P=C1,AC∩AM=A,
所以平面A1PC1∥平面AMC.…(14分)
(Ⅰ)证明:在正四棱柱ABCD-A1B1C1D1中,连结BD交AC于N,连结MN.
因为ABCD为正方形,所以N为BD中点.…(1分)
在△DBD1中,因为M为DD1中点,
所以BD1∥MN.…(2分)
因为MN?平面AMC,BD1不包含于平面AMC,…(4分)
所以BD1∥平面AMC.…(5分)
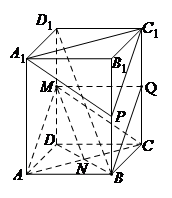 (Ⅱ)证明因为ABCD为正方形,
(Ⅱ)证明因为ABCD为正方形,所以AC⊥BD.…(6分)
因为DD1⊥平面ABCD,
所以DD1⊥AC.…(7分)
因为DD1∩BD=D,…(8分)
所以AC⊥平面BDD1.…(9分)
因为BD1?平面BDD1,
所以AC⊥BD1.…(10分)
(Ⅲ)解:当λ=
| 1 |
| 2 |
因为AA1∥CC1,且AA1=CC1,
所以四边形AA1C1C是平行四边形.
所以AC∥A1C1.…(12分)
取CC1的中点Q,连结MQ,QB.
因为M为DD1中点,
所以MQ∥AB,且MQ=AB,
所以四边形ABQM是平行四边形.
所以BQ∥AM.…(13分)
同理BQ∥C1P.
所以AM∥C1P.
因为A1C1∩C1P=C1,AC∩AM=A,
所以平面A1PC1∥平面AMC.…(14分)
点评:本题考查直线与平面平行的证明,考查异面直线垂直的证明,考查满足平面与平面平行的点是否存在的判断与求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
 如图,圆周上有n个固定点,分别为A1,A2,…,An(n∈N*,n≥2),在每一个点上分别标上1,2,3中的某一个数字,但相邻的两个数字不相同,记所有的标法总数为an.
如图,圆周上有n个固定点,分别为A1,A2,…,An(n∈N*,n≥2),在每一个点上分别标上1,2,3中的某一个数字,但相邻的两个数字不相同,记所有的标法总数为an.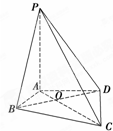 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BAD=120°,AD=AB=1,AC交BD于O点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BAD=120°,AD=AB=1,AC交BD于O点. 如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,PD⊥AC于点D,且DC=2AD=2,E为PC上一点,PE:EC=1:2,
如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,PD⊥AC于点D,且DC=2AD=2,E为PC上一点,PE:EC=1:2,