题目内容
试求关于x的函数y=-x2+mx+2在0≤x≤2上的最大值.
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:讨论对称轴去区间之间的关系,结合二次函数的性质即可求出函数的最大值.
解答:
解:函数y=f(x)=-x2+mx+2=-(x-
)2+
+2,
若对称轴x=
≤0,即m≤0时,函数在0≤x≤2上单调递减,此时函数的最大值为f(0)=2,
对称轴x=
≥2,即m≥4时,函数在0≤x≤2上单调递增,此时函数的最大值为f(2)=2m-2,
若0≤
≤2,即0≤m≤4,此时函数的最大值为f(
)=
+2.
综上:当m≤0时,最大值为2,
当m≥4时,最大值为2m-2,
当0≤m≤4,函数的最大值为f(
)=
+2.
| m |
| 2 |
| m2 |
| 4 |
若对称轴x=
| m |
| 2 |
对称轴x=
| m |
| 2 |
若0≤
| m |
| 2 |
| m |
| 2 |
| m2 |
| 4 |
综上:当m≤0时,最大值为2,
当m≥4时,最大值为2m-2,
当0≤m≤4,函数的最大值为f(
| m |
| 2 |
| m2 |
| 4 |
点评:本题主要考查二次函数的最值问题,讨论对称轴和对称区间之间的关系是解决本题的关键.

练习册系列答案
相关题目
函数f(x)=x2+x+b,函数g(x)=ex-f′(x)的零点所在的区间是[k,k+1](k∈Z),则k的值等于( )
| A、-1 | B、0 | C、1 | D、0或1 |
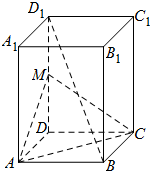 已知正四棱柱ABCD-A1B1C1D1中,M是DD1的中点.
已知正四棱柱ABCD-A1B1C1D1中,M是DD1的中点.