题目内容
过点F1(-
,0),F2(
,0),△ABC内切圆心在直线x=1,x=-1上移动,
(1)求顶点C的轨迹方程;
(2)过圆x2+y2=2上一点的切线l交轨迹C于点A,B两点,求证:∠AOB为定值.
| 3 |
| 3 |
(1)求顶点C的轨迹方程;
(2)过圆x2+y2=2上一点的切线l交轨迹C于点A,B两点,求证:∠AOB为定值.
考点:轨迹方程,圆的切线方程
专题:圆锥曲线的定义、性质与方程
分析:(1)由题意画出图形,利用圆的切线长相等得到C满足|CF1|-|CF2|=±2,从而求得双曲线方程;
(2)设出切点P的坐标,表示出过切点的圆x2+y2=2的方程,和双曲线方程联立后利用根与系数的关系得到两焦点A,B的横纵坐标的积,代入数量积公式得答案.
(2)设出切点P的坐标,表示出过切点的圆x2+y2=2的方程,和双曲线方程联立后利用根与系数的关系得到两焦点A,B的横纵坐标的积,代入数量积公式得答案.
解答:
(1)解:如图,
 设切点分别为D、E、F,内心在直线x=1上时,则|CF1|-|CF2|=|F1E|-|F2F|=|F1D|-|F2D|=(
设切点分别为D、E、F,内心在直线x=1上时,则|CF1|-|CF2|=|F1E|-|F2F|=|F1D|-|F2D|=(
+1)-(
-1)=2,
同理,内心在x=-1上时,|CF1|-|CF2|=-2,
故|CF1|-|CF2|=±2,
∴C的方程为x2-
=1(y≠0);
(2)证明:设切点P(x0,y0),l与轨迹C交于A(x1,y1),B(x2,y2),则l方程为x0x+y0y=2,
由
⇒(2
-
)x2+4x0x-(2
+4)=0,
当y0≠0时,2
-
≠0,
∴x1+x2=-
,x1x2=-
,
又y1y2=
•
=
,x02+y02=2,
∴
•
=x1x2+y1y2=
=0,
∴OA⊥OB⇒∠AOB=90°;
当y0=0时,上述结论仍成立,综上可知∠AOB=90°.
 设切点分别为D、E、F,内心在直线x=1上时,则|CF1|-|CF2|=|F1E|-|F2F|=|F1D|-|F2D|=(
设切点分别为D、E、F,内心在直线x=1上时,则|CF1|-|CF2|=|F1E|-|F2F|=|F1D|-|F2D|=(| 3 |
| 3 |
同理,内心在x=-1上时,|CF1|-|CF2|=-2,
故|CF1|-|CF2|=±2,
∴C的方程为x2-
| y2 |
| 2 |
(2)证明:设切点P(x0,y0),l与轨迹C交于A(x1,y1),B(x2,y2),则l方程为x0x+y0y=2,
由
|
| y | 2 0 |
| x | 2 0 |
| y | 2 0 |
当y0≠0时,2
| y | 2 0 |
| x | 2 0 |
∴x1+x2=-
| 4x0 | ||||
2
|
2
| ||||
2
|
又y1y2=
| 2-x0x1 |
| y0 |
| 2-x0x2 |
| y0 |
8-2
| ||||
2
|
∴
| OA |
| OB |
| 4-2(x02+y02) | ||||
2
|
∴OA⊥OB⇒∠AOB=90°;
当y0=0时,上述结论仍成立,综上可知∠AOB=90°.
点评:本题考查了双曲线的定义,考查了双曲线的标准方程,体现了数学转化思想方法和数形结合的解题思想方法,考查了直线与圆锥曲线的关系,是中档题.

练习册系列答案
相关题目
将函数f(x)=3sin(2x+
)-1的图形按向量
=(m,n)平移后得到函数g(x)=3sin2x的图形则向量
的一个可能值是( )
| π |
| 3 |
| a |
| a |
A、(-
| ||
B、(-
| ||
C、(
| ||
D、(
|
下列函数中,在其定义域上为减函数的是( )
A、y=x
| ||
B、y=(
| ||
| C、y=sinx | ||
| D、y=log2x |
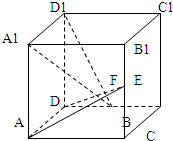 如果正方体ABCD-A1B1C1D1中EF分别是BB1、CD中点.
如果正方体ABCD-A1B1C1D1中EF分别是BB1、CD中点.