Question

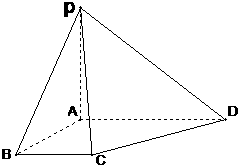
如图1，在直角梯形ABCD中，AD∥BC，AB=2，BC=4，∠ABC=60°，沿对角线AC将梯形折成几何体PACD，并使得∠PAD=90°（如图2所示）．
（Ⅰ）求证：PA⊥平面ACD；
（Ⅱ）若O为几何体PACD外接球的球心，点G为△PCD的重心，求几何体OACDG的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,直线与平面垂直的判定

专题：计算题,空间位置关系与距离

分析：（Ⅰ）运用余弦定理和勾股定理，证得AB⊥AC，再由折叠的特点，即可证得PA⊥平面ACD；
（Ⅱ）运用面面垂直的性质定理，以及线面垂直的性质和判断，得到OE⊥平面ACD，通过解直角梯形ABCD，再由棱锥体积公式，即可得到．

解答： （Ⅰ）证明：在梯形ABCD中，AB=2，BC=4，∠ABC=60°，
则AC=

4+16-2×2×4× 1 2

=2

3

，
从而BC²=AC²+AB²，即有AB⊥AC，
在几何体PACD中，PA⊥AC，又PA⊥AD，
则PA⊥平面ACD；
（Ⅱ）解：PA⊥平面ACD，PA?平面PAD，
则平面PAD⊥平面ACD，
由AD⊥CD，则CD⊥平面PAD，即CD⊥PD，
则三角形PAC，PCD均为直角三角形，
该几何体PACD的外接球的球心O为PC的中点，由于G为三角形PCD的重心，
则O，G，D三点共线，取AC的中点E，连接OE，则OE∥PA，OE=

1

2

PA=1，
由于PA⊥平面ACD，则OE⊥平面ACD，
在直角梯形ABCD中，AD∥BC，AB=2，BC=4，∠ABC=60°，
则CD=ABsin60°=

3

，AD=4-ABcos60°=3，
则有V_O-ACD=

1

3

×1×(

1

2

×3×

3

)=

3

2

．

点评：本题考查面面垂直的性质和线面垂直的性质和判定定理及运用，考查棱锥体积公式的运用，考查运算能力，属于中档题．