题目内容
已知集合A={x|-1＜x＜2}，B={x|x＜a}．
（Ⅰ）若a=1，求A∩B；
（Ⅱ）若A∩B=A，求实数a的取值范围．
（Ⅰ）若a=1，求A∩B；
（Ⅱ）若A∩B=A，求实数a的取值范围．
考点：交集及其运算
专题：集合
分析：（Ⅰ）把a=1代入B，确定出B，求出A∩B即可；
（Ⅱ）由A∩B=A，得到A为B的子集，求出a的范围即可．
（Ⅱ）由A∩B=A，得到A为B的子集，求出a的范围即可．
解答：
解：（Ⅰ）把a=1代入B中得：B={x|x＜1}，
∵A={x|-1＜x＜2}，
∴A∩B={x|-1＜x＜1}；
（Ⅱ）∵A∩B=A，∴A⊆B，
∴实数a的范围为a＞2．
∵A={x|-1＜x＜2}，
∴A∩B={x|-1＜x＜1}；
（Ⅱ）∵A∩B=A，∴A⊆B，
∴实数a的范围为a＞2．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
在平面直角坐标系中，已知向量
=（1，-2），
-
=（2，-3），
=（x，9），若（2
+
）∥
，则x=（ ）
| a |
| a |
| b |
| c |
| a |
| b |
| c |
| A、-2 | B、-4 | C、-3 | D、-1 |
已知函数f（x）=
，则f[f(
)]的值为（ ）
|
| 1 |
| 4 |
A、
| ||
B、
| ||
| C、-2 | ||
| D、3 |
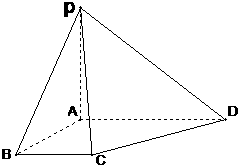如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，∠BAD=90°，BC∥AD，PA⊥底面ABCD，BC=AB=1，PA=AD=2