题目内容

函数y=sin2x+2
3
sin2x的最小正周期T为（　　）
A、π
B、2π
C、
π
2
D、
π
4
考点：两角和与差的正弦函数,三角函数的周期性及其求法
专题：三角函数的求值,三角函数的图像与性质
分析：化简可得y═2sin（2x-
π
3
）+
3
，从而可由正弦函数的周期公式即可解得．
解答： 解：∵y=sin2x+2
3
sin2x
=sin2x+2
3
×
1-cos2x
2

=sin2x-
3
cos2x+
3

=2sin（2x-
π
3
）+
3

∴T=
2π
2
=π
故选：A．
点评：本题主要考察了两角和与差的正弦函数，三角函数的周期性及其求法，属于基本知识的考查．
练习册系列答案
相关题目
已知△ABC内角A，B，C的对边分别为a，b，c，a=
2
，b=
3
，B=60°，则角A等于（　　）
A、30°B、45°
C、60°D、90°
若函数f（x）=
x+a
bx+1
为区间[-1，1]上的奇函数，求a，b的值．
下列不等式成立的是（其中a＞0且a≠1）（　　）
A、loga5.1＜loga5.9
B、1.70.3＞0.93.1
C、a0.8＜a0.9
D、log32.9＜log0.52.2
已知函数f（x）=
1
x
-2xn，且f（2）=-
7
2

（1）求n；
（2）判断f（x）的奇偶性；
（3）试判断f（x）在（0，+∞）上的单调性，并证明．
设m，n∈R，且msinα+ncosα=5，则
m2+n2
的最小值为
 
．
已知函数f（x）=loga(
2-x
2+x
)，且f(-
2
3
)=1．
（Ⅰ）求a的值和函数f（x）的定义域；
（Ⅱ）判断函数f（x）的奇偶性，并证明．
在平面直角坐标系中，已知向量
a
=（1，-2），
a
-
b
=（2，-3），
c
=（x，9），若（2
a
+
b
）∥
c
，则x=（　　）
A、-2B、-4C、-3D、-1
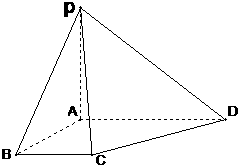如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，∠BAD=90°，BC∥AD，PA⊥底面ABCD，BC=AB=1，PA=AD=2
（1）证明：AB⊥PD；
（2）求直线AB与直线PC夹角的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网