题目内容
已知tanα=2,并且α是第三象限角
(Ⅰ)求sinα和cosα的值.
(Ⅱ)求sin(α+
)•sin(π-α)的值.
(Ⅰ)求sinα和cosα的值.
(Ⅱ)求sin(α+
| π |
| 2 |
考点:运用诱导公式化简求值,同角三角函数基本关系的运用
专题:三角函数的求值
分析:(Ⅰ)求sinα和cosα的值.
(Ⅱ)求sin(α+
)•sin(π-α)的值.
(Ⅱ)求sin(α+
| π |
| 2 |
解答:
解:(Ⅰ)因为tanα=2,所以
=2,代入sin2α+cos2α=1,
可得cosα=±
,并且α是第三象限角,
∴cosα=-
,sinα=-
.
(Ⅱ)sin(α+
)•sin(π-α)=cosαsinα=-
×(-
)=
.
| sinα |
| cosα |
可得cosα=±
| ||
| 5 |
∴cosα=-
| ||
| 5 |
2
| ||
| 5 |
(Ⅱ)sin(α+
| π |
| 2 |
2
| ||
| 5 |
| ||
| 5 |
| 2 |
| 5 |
点评:本题考查三角函数的化简求值,同角三角函数的基本关系式,条件诱导公式的应用,基本知识的考查.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
下列函数中,表示同一函数的一组是( )
A、f(x)=
| |||||||
| B、f(x)=lg(x(x+1)),g(x)=lgx+lg(x+1) | |||||||
| C、f(x)=x-1(x∈R),g(x)=x-1(x∈N) | |||||||
| D、f(x)=x2+x-1,g(x)=t2+t-1 |
若过点A(0,-1)的直线l与圆x2+(y-3)2=4的圆心的距离记为d,则d的取值范围为( )
| A、[0,4] |
| B、[0,3] |
| C、[0,2] |
| D、[0,1] |
设向量
=(2,0),
=(1,1),则下列结论中正确的是( )
| a |
| b |
A、
| ||||
B、|
| ||||
C、
| ||||
D、
|
已知函数f(x)=
,若f(a)+f(1)=0,则实数a的值为( )
|
| A、-3 | B、-2 | C、-1 | D、1 |
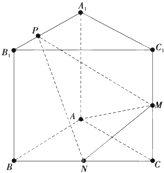 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=2,AB⊥AC,M、N分别是CC1、BC的中点,点P在线段A1B1上,且
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=2,AB⊥AC,M、N分别是CC1、BC的中点,点P在线段A1B1上,且