题目内容
15.设A,B,C,D为平面内的四点,且A(1,3),B(2,-2),C(4,1)(Ⅰ)若$\overrightarrow{AB}$=$\overrightarrow{CD}$,求D点的坐标及|$\overrightarrow{AD}$|;
(Ⅱ)设向量$\overrightarrow{a}$=$\overrightarrow{AB}$,$\overrightarrow{b}$=$\overrightarrow{BC}$,若k$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{a}$+3$\overrightarrow{b}$平行,求实数k的值.
分析 (Ⅰ)设出D的坐标,得到$\overrightarrow{AB}、\overrightarrow{CD}$的坐标,结合$\overrightarrow{AB}$=$\overrightarrow{CD}$列式求得D的坐标,得到$\overrightarrow{AD}$,则|$\overrightarrow{AD}$|可求;
(Ⅱ)由$\overrightarrow{a}、\overrightarrow{b}$的坐标得到k$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{a}$+3$\overrightarrow{b}$的坐标,再由向量共线的坐标运算列式求得k值.
解答 解:(Ⅰ)设D(x,y),
由A(1,3),B(2,-2),C(4,1),
得$\overrightarrow{AB}$=(1,-5),$\overrightarrow{CD}=(x-4,y-1)$,
∵$\overrightarrow{AB}=\overrightarrow{CD}$,∴$\left\{\begin{array}{l}{x-4=1}\\{y-1=-5}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=5}\\{y=-4}\end{array}\right.$,
∴D(5,-4).
∴$\overrightarrow{AD}=(4,-7)$,则|$\overrightarrow{AD}$|=$\sqrt{{4}^{2}+(-7)^{2}}=\sqrt{65}$;
(Ⅱ)∵$\overrightarrow{a}$=$\overrightarrow{AB}$=(1,-5),$\overrightarrow{b}$=$\overrightarrow{BC}$=(2,3),
∴$k\overrightarrow{a}-\overrightarrow{b}=(k-2,-5k-3)$,$\overrightarrow{a}+3\overrightarrow{b}=(7,4)$,
又∵k$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{a}$+3$\overrightarrow{b}$平行,
∴4(k-2)-7(-5k-3)=0,得k=-$\frac{1}{3}$.
∴k的值为-$\frac{1}{3}$.
点评 本题考查平面向量的数量积运算,考查向量共线的坐标表示,是基础题.

| A. | 60°或120° | B. | 30°或150° | C. | 60° | D. | 30° |
| A. | $[{-1,\frac{1}{4}}]$ | B. | $[{\frac{1}{4},1}]$ | C. | $[{-2,\frac{1}{4}}]$ | D. | $[{\frac{1}{3},1}]$ |
| A. | a≥15 | B. | a>15 | C. | a<5 | D. | a≤5 |
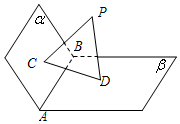 如图,已知平面α,β,且α∩β=AB,PC⊥α,PD⊥β,C,D是垂足.
如图,已知平面α,β,且α∩β=AB,PC⊥α,PD⊥β,C,D是垂足. 如图,公园有一块边长为2的等边三角形△ABC的地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
如图,公园有一块边长为2的等边三角形△ABC的地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.