题目内容
已知点A在抛物线y2=4x上，且点A到直线x-y-1=0的距离为
，则点A的个数为（ ）
| 2 |
| A、1 | B、2 | C、3 | D、4 |
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据点A到直线x-y-1=0的距离为
，列出方程，解方程可得结论．
| 2 |
解答：
解：设A（x，y），
∵点A到直线x-y-1=0的距离为
，
∴
=
∴|x-y-1|=2，
当x-y-1=2，即
-y-3=0，方程有两解；
x-y-1=-2，即
-y+1=0，方程有一解，
∴满足条件的点A有3个．
故选：C．
∵点A到直线x-y-1=0的距离为
| 2 |
∴
| |x-y-1| | ||
|
| 2 |
∴|x-y-1|=2，
当x-y-1=2，即
| y2 |
| 4 |
x-y-1=-2，即
| y2 |
| 4 |
∴满足条件的点A有3个．
故选：C．
点评：本题考查抛物线方程，考查点到直线距离公式的运用，属于基础题．
练习册系列答案
芒果教辅达标测试卷系列答案
相关题目
若函数f（x）为奇函数，且当x＞0时，f（x）=x-1，则当x＜0时，有（ ）
| A、f（x）＞0 |
| B、f（x）＜0 |
| C、f（x）f（-x）≤0 |
| D、f（x）-f（-x）＞0 |
集合A={x|y=
}，集合B={y|y=-
}，则有（ ）
| 1 | ||
|
| 1 | ||
|
| A、A⊆B | B、A∩B=∅ |
| C、B⊆A | D、以上均错误 |
若二项式（
+x2）3展开式中的常数项为k，则直线y=kx与曲线y=x2围成的封闭图形的面积为（ ）
| 1 |
| x |
| A、3 | ||
B、
| ||
| C、9 | ||
D、
|
已知f（x）=
是（-∞，+∞）上的减函数，那么a的取值范围是（ ）
|
| A、（-∞，1] | ||||
B、[
| ||||
| C、[0，1] | ||||
D、（
|
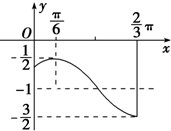如图，是函数y=Asin（ωx+φ）+k（A＞0，ω＞0，|φ|＜