题目内容
5.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的短轴一个端点到右焦点F的距离为2,且过点$({-1,-\frac{{\sqrt{3}}}{2}})$.(1)求椭圆C的方程;
(2)设M,N为椭圆C上不同的两点,A,B分别为椭圆C上的左右顶点,直线MN既不平行与坐标轴,也不过椭圆C的右焦点F,若∠AFM=∠BFN,求证:直线MN过定点.
分析 (1)由题意可知:a=2,将点代入椭圆方程,即可求得b的值,即可求得椭圆方程;
(2)设直线MN的方程y=k1x+m,代入椭圆方程,由韦达定理,及kFM+kFN=0,即可求得m=-$\frac{4\sqrt{3}}{3}$k1,直线MN的方程为y=k1(x-$\frac{4\sqrt{3}}{3}$),则直线MN过定点($\frac{4\sqrt{3}}{3}$,0).
解答 解:(1)由题意可知:短轴一个端点到右焦点F的距离为2,则a=2,
将$({-1,-\frac{{\sqrt{3}}}{2}})$代入椭圆方程可得$\frac{1}{4}+\frac{3}{4{b}^{2}}=1$,解得:b2=1,
∴椭圆的标准方程:$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(2)证明:由(1)可知:F($\sqrt{3}$,0),
设直线MN的方程y=k1x+m,(k≠0),M(x1,y1),N(x2,y2).
则$\left\{\begin{array}{l}{y={k}_{1}x+m}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,整理得:(1+2k12)x2+8k1mx+4m2-4=0,
x1+x2=-$\frac{8{k}_{1}m}{1+4{k}_{1}^{2}}$,x1x2=$\frac{4{m}^{2}-4}{1+4{k}_{1}^{2}}$,
由∠AFM=∠BFN,则kFM+kFN=0,$\frac{{y}_{1}}{{x}_{1}-\sqrt{3}}$+$\frac{{y}_{2}}{{x}_{2}-\sqrt{3}}$=0,
(k1x1+m)(x2-$\sqrt{3}$)+(k1x2+m)(x1-$\sqrt{3}$)=0,
整理得:2k1x1x2-(m-$\sqrt{3}$k1)(x1+x2)-2$\sqrt{3}$m=0,
则2k1×$\frac{4{m}^{2}-4}{1+4{k}_{1}^{2}}$-(m-$\sqrt{3}$k1)(-$\frac{8{k}_{1}m}{1+4{k}_{1}^{2}}$)-2$\sqrt{3}$m=0,
解得:m=-$\frac{4\sqrt{3}}{3}$k1,
∴直线MN的方程为y=k1(x-$\frac{4\sqrt{3}}{3}$),
则直线MN过定点($\frac{4\sqrt{3}}{3}$,0).
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,直线的斜率公式,考查计算能力,属于中档题.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案| A. | (-∞,-2)∪(2,+∞) | B. | (-∞,-,4)∪(4,+∞) | C. | (-2,2) | D. | (-4,4) |
| A. | 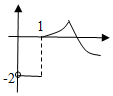 | B. | 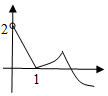 | C. | 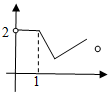 | D. | 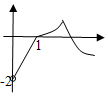 |
| A. | x+y-2=0 | B. | y-1=0 | C. | x+3y-4=0 | D. | x-y=0 |
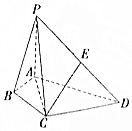 如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2,AB=1.
如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2,AB=1.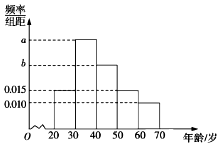 根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.
根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.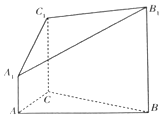 如图,在几何体A1B1C1-ABC中,△ABC为等边三角形,AA1⊥平面ABC,AA1∥BB1∥CC1,BB1:CC1:AA1=3:2:1
如图,在几何体A1B1C1-ABC中,△ABC为等边三角形,AA1⊥平面ABC,AA1∥BB1∥CC1,BB1:CC1:AA1=3:2:1