题目内容
15.已知向量$\overrightarrow{a}$=(m,2),$\overrightarrow{b}$=(2,-1),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则$\frac{|2\overrightarrow{a}-\overrightarrow{b}|}{\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})}$等于( )| A. | $-\frac{5}{3}$ | B. | 1 | C. | 2 | D. | $\frac{5}{4}$ |
分析 依题意,由$\overrightarrow{a}$•$\overrightarrow{b}$=2m-2=0⇒m=1,即$\overrightarrow{a}$=(1,2),于是可得2$\overrightarrow{a}$-$\overrightarrow{b}$=(0,5),|2$\overrightarrow{a}$-$\overrightarrow{b}$|=5,$\overrightarrow{a}$+$\overrightarrow{b}$=(3,1),$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=1×3+2×1=5,从而可得$\frac{|2\overrightarrow{a}-\overrightarrow{b}|}{\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})}$的值.
解答 解:∵$\overrightarrow{a}$=(m,2),$\overrightarrow{b}$=(2,-1),
且$\overrightarrow{a}$⊥$\overrightarrow{b}$,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=2m-2=0,
∴m=1,
∴$\overrightarrow{a}$=(1,2),2$\overrightarrow{a}$-$\overrightarrow{b}$=(0,5),|2$\overrightarrow{a}$-$\overrightarrow{b}$|=5,
又$\overrightarrow{a}$+$\overrightarrow{b}$=(3,1),$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=1×3+2×1=5,
∴$\frac{|2\overrightarrow{a}-\overrightarrow{b}|}{\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})}$=$\frac{5}{5}$=1.
故选:B.
点评 本题考查平面向量数量积的坐标运算,求得m=1及2$\overrightarrow{a}$-$\overrightarrow{b}$=(0,5)、$\overrightarrow{a}$+$\overrightarrow{b}$=(3,1)是关键,考查运算求解能力,属于中档题.

 初中学业考试导与练系列答案
初中学业考试导与练系列答案| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
| A. | (-∞,-1) | B. | (4,+∞) | C. | (-1,4) | D. | (-4,-1) |
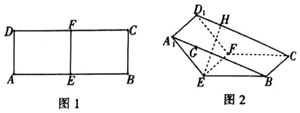 如图1,在矩形ABCD中,AB=8,AD=3,点E,F分别为AB、CD的中点,将四边形AEFD沿EF折到A1EFD1的位置,使∠A1EB=120°,如图2所示,点G、H分别在A1B、D1C上,A1G=D1H=$\sqrt{3}$,过点G、H的平面α与几何体A1EB-D1FC的面相交,交线围成一个正方形.
如图1,在矩形ABCD中,AB=8,AD=3,点E,F分别为AB、CD的中点,将四边形AEFD沿EF折到A1EFD1的位置,使∠A1EB=120°,如图2所示,点G、H分别在A1B、D1C上,A1G=D1H=$\sqrt{3}$,过点G、H的平面α与几何体A1EB-D1FC的面相交,交线围成一个正方形.