题目内容

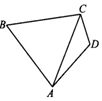
17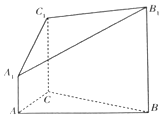．如图，在几何体A1B1C1-ABC中，△ABC为等边三角形，AA1⊥平面ABC，AA1∥BB1∥CC1，BB1：CC1：AA1=3：2：1
（Ⅰ）求证：平面A1B1C1⊥平面A1ABB1；
（Ⅱ）F为线段BB1上一点，当A1B1∥平面ACF时，求$\frac{{B}_{1}F}{{B}_{1}B}$的值．

分析 （Ⅰ）：取A1B1，AB的中点M，N，连接C1M，CN，MN，只需证明四边形C1MNC是平行四边形，即可得到C1M⊥平面A1ABB1 ，平面A1B1C1⊥平面A1ABB1
（Ⅱ）可得四边形A1AFB1是平行四边形，即B1F=AA1，由BB1：AA1=3：1，得$\frac{{B}_{1}F}{{B}_{1}B}$=$\frac{1}{3}$．

解答 解：（Ⅰ）证明：取A1B1，AB的中点M，N，连接C1M，CN，MN，
∴AA1∥BB1∥MN，CC1∥MN；
又因为$MN=\frac{A{A}_{1}+B{B}_{1}}{2}$，BB1：CC1：AA1=3：2：1
所以$C{C}_{1}=\frac{A{A}_{1}+B{B}_{1}}{2}=MN$，即四边形C1MNC是平行四边形，∴C1M∥CN
又AA1⊥平面ABC，∴平面ABC⊥平面A1ABB1，
∵平面A1B1C1∩平面A1ABB1=AB，又CN⊥AB，∴CN⊥平面A1ABB1
∴C1M⊥平面A1ABB1 ，又C1M平面A1B1C1
∴平面A1B1C1⊥平面A1ABB1
（Ⅱ）∵A1B1∥平面ACF，A1B1?平面A1ABB1，面ACF∩平面A1ABB1，∴A1B1∥AF．
又AA1∥BB1，所以四边形A1AFB1是平行四边形，∴B1F=AA1，因为BB1：AA1=3：1．
∴$\frac{{B}_{1}F}{{B}_{1}B}$=$\frac{1}{3}$，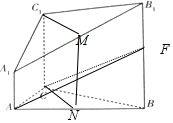

点评 本题考查了空间面面平行的判定，线面平行的性质，转化思想，属于中档题，

练习册系列答案
相关题目
7．已知等轴双曲线C的一个焦点是F1（-6，0），点M是等轴双曲线的渐近线上的一个动点，点P是圆（x+6）2+y2=1上的任意一点，则|PM|的最小值是（　　）
A．3$\sqrt{2}$-1B．2$\sqrt{3}$-1C．3$\sqrt{3}$+1D．2$\sqrt{3}$+2
8．在△ABC中，角A、B、C所对的边分别为a，b，c，满足（2a-c）cosB=bcosC．
（1）求B的大小；
（2）如图，AB=AC，在直线AC的右侧取点D，使得AD=2CD=4．当角D为何值时，四边形ABCD面积最大．
5．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的短轴一个端点到右焦点F的距离为2，且过点$（{-1，-\frac{{\sqrt{3}}}{2}}）$．
（1）求椭圆C的方程；
（2）设M，N为椭圆C上不同的两点，A，B分别为椭圆C上的左右顶点，直线MN既不平行与坐标轴，也不过椭圆C的右焦点F，若∠AFM=∠BFN，求证：直线MN过定点．
12．已知函数f（x）=x（a-$\frac{1}{e^x}$），曲线y=f（x）上存在两个不同点，使得曲线在这两点处的切线都与y轴垂直，则实数a的取值范围是（　　）
A．（-e2，+∞）B．（-e2，0）C．（-$\frac{1}{e^2}$，+∞）D．（-$\frac{1}{e^2}$，0）
2．函数$f（x）=\frac{1}{2}cos（ωx+φ）$（ω＞0，$|φ|＜\frac{π}{2}$）的部分图象如图所示，则φ的值为（　　）
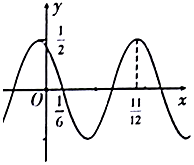
A．$\frac{π}{3}$B．$\frac{π}{6}$C．$-\frac{π}{6}$D．$-\frac{π}{3}$
9．某程序框图如图所示，则该程序运行后输出的值是（　　）
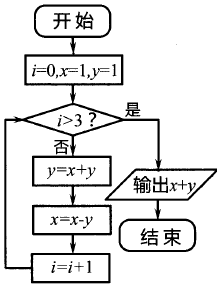
A．0B．-1C．-2D．-8
6．已知抛物线C：y2=4x的焦点为F，准线为l．⊙F与C交于A，B两点，与x轴的负半轴交于点P．
（Ⅰ）若⊙F被l所截得的弦长为$2\sqrt{5}$，求|AB|；
（Ⅱ）判断直线PA与C的交点个数，并说明理由．
7．已知复数$z=\frac{{a+2{i^3}}}{2-i}$在复平面内对应的点在第四象限，则实数a的取值范围是（　　）
A．（-∞，-1）B．（4，+∞）C．（-1，4）D．（-4，-1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网