题目内容
已知方程x2+y2-2mx+2my-2=0表示的曲线恒过第三象限的一个定点A,若点A又在直线l:mx+ny+1=0上,则当正数m,n的乘积取得最大值时直线l的方程是 .
考点:直线和圆的方程的应用
专题:计算题
分析:先根据方程x2+y2-2mx+2my-2=0,确定第三象限的定点A的坐标,代入直线l:mx+ny+1=0上,利用基本不等式,可求正数m,n的乘积的最大值,故可求直线方程.
解答:
解:∵方程x2+y2-2mx+2my-2=0
∴x2+y2-2-2m(x-y)=0
解方程组
得
或
∵A在第三象限
∴A(-1,-1)
∵点A在直线l:mx+ny+1=0
∴m+n=1
∵m>0,n>0
∴mn≤(
)2=
当且仅当m=n=
时,正数m,n的乘积取得最大值
∴直线l:mx+ny+1=0为直线l:x+y+2=0
故答案为:x+y+2=0
∴x2+y2-2-2m(x-y)=0
解方程组
|
得
|
|
∵A在第三象限
∴A(-1,-1)
∵点A在直线l:mx+ny+1=0
∴m+n=1
∵m>0,n>0
∴mn≤(
| m+n |
| 2 |
| 1 |
| 4 |
当且仅当m=n=
| 1 |
| 2 |
∴直线l:mx+ny+1=0为直线l:x+y+2=0
故答案为:x+y+2=0
点评:本题以圆的方程为载体,考查定点问题,考查基本不等式的运用,解题的关键是根据圆的方程确定定点的坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将4个不相同的小球放入编号为1、2、3的3个盒子中,当某个盒子中球的个数等于该盒子编号时称为一个和谐盒,则恰有两个和谐盒的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知实数k满足
>1.则方程x2-kx+1=0的两个根可分别作为( )
| 1 |
| k-2 |
| A、一椭圆和一双曲线的离心率 |
| B、两抛物线的离心率 |
| C、一椭圆和一抛物线的离心率 |
| D、两椭圆的离心率 |
设f(x)是定义域为R的奇函数,且在(0,+∞)上是减函数,若f(1)=0,则不等式f(x)>0的解集是( )
| A、(-∞,-1)∪(1,+∞) |
| B、(-1,0)∪(0,1) |
| C、(-∞,-1)∪(0,1) |
| D、(-1,0)∪(1,+∞) |
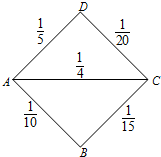 某先生居住在城镇的A处,准备开车到单位C处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如下图(例如,路段AB发生堵车事件的概率为
某先生居住在城镇的A处,准备开车到单位C处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如下图(例如,路段AB发生堵车事件的概率为