题目内容
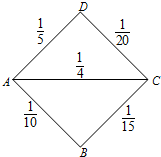 某先生居住在城镇的A处,准备开车到单位C处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如下图(例如,路段AB发生堵车事件的概率为
某先生居住在城镇的A处,准备开车到单位C处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如下图(例如,路段AB发生堵车事件的概率为| 1 |
| 10 |
| 1 |
| 15 |
(1)请你为其选择一条由A到C的路线,使得途中发生堵车事件的概率最小;
(2)若记路线A→B→C中遇到堵车次数为随机变量ξ,求ξ的数学期望Eξ.
考点:离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题:计算题
分析:(1)因为各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,所以路线A→C中遇到堵车的概率P1可以做出,路线A→D→C中遇到堵车的概率P2,路线A→B→C中遇到堵车的概率P3,进行比较得到结果.
(2)由题意知路线A→B→C中遇到堵车次数X可取值为0,1,2.结合变量对应的事件,能够求出变量的期望.
(2)由题意知路线A→B→C中遇到堵车次数X可取值为0,1,2.结合变量对应的事件,能够求出变量的期望.
解答:
解:∵各路段发生堵车事件都是独立的,
且在同一路段发生堵车事件最多只有一次,
∴路线A→C中遇到堵车的概率P1=
;
路线A→D→C中遇到堵车的概率P2=1-(1-
)(1-
)=
;
路线A→B→C中遇到堵车的概率P3=1-(1-
)(1-
)=
.
∴路线A→B→C中遇到堵车的概率最小.
(2)由题意知路线A→B→C中遇到堵车次数X可取值为0,1,2.
P(X=0)=(1-
)(1-
)=
,
P(X=1)=
×(1-
) +(1-
)×
=
,
P(X=2)=
×
=
.
∴EX=0×
+1×
+2×
=
.
且在同一路段发生堵车事件最多只有一次,
∴路线A→C中遇到堵车的概率P1=
| 1 |
| 4 |
路线A→D→C中遇到堵车的概率P2=1-(1-
| 1 |
| 5 |
| 1 |
| 20 |
| 6 |
| 25 |
路线A→B→C中遇到堵车的概率P3=1-(1-
| 1 |
| 10 |
| 1 |
| 15 |
| 4 |
| 25 |
∴路线A→B→C中遇到堵车的概率最小.
(2)由题意知路线A→B→C中遇到堵车次数X可取值为0,1,2.
P(X=0)=(1-
| 1 |
| 10 |
| 1 |
| 15 |
| 21 |
| 25 |
P(X=1)=
| 1 |
| 10 |
| 1 |
| 15 |
| 1 |
| 10 |
| 1 |
| 15 |
| 23 |
| 150 |
P(X=2)=
| 1 |
| 10 |
| 1 |
| 15 |
| 1 |
| 150 |
∴EX=0×
| 21 |
| 25 |
| 23 |
| 150 |
| 1 |
| 150 |
| 1 |
| 6 |
点评:本题考查离散型随机变量的分布列和期望问题,考查相互独立事件同时发生的概率,求离散型随机变量的分布列和期望是近年来理科高考必出的一个问题,题目做起来不难.

练习册系列答案
相关题目
下列计算正确的是( )
| A、a6÷a6=0 |
| B、(-bc)4÷(-bc)2=-bc |
| C、y4+y6=y10 |
| D、(ab4)4=a4b16 |