题目内容
9.以抛物线x2=4y的焦点F为圆心的圆交抛物线于A、B两点,交抛物线的准线于C、D两点,若四边形ABCD是矩形,则圆的方程为( )| A. | x2+(y-1)2=3 | B. | x2+(y-1)2=4 | C. | x2+(y-1)2=12 | D. | x2+(y-1)2=16 |
分析 连接AC,BD,抛物线的定义与性质求出圆心坐标为F(0,1),|FA|=|FB|,设圆的半径r,∠FAB=θ,则A(rcosθ,1+rsinθ),而A在抛物线上,化简求解即可.
解答  解:如图,连接AC,BD,抛物线x2=4y的焦点坐标(0,1),
解:如图,连接AC,BD,抛物线x2=4y的焦点坐标(0,1),
由抛物线的定义与性质可知圆心坐标为F(0,1),|FA|=|FB|,设圆的半径r,
∠FAB=θ,则A(rcosθ,1+rsinθ),而A在抛物线上,
故r2cos2θ=4+4rsinθ,又rsinθ=2,所以$sinθ=\frac{1}{2}$,$θ=\frac{π}{6}$,∴r=4,
所求圆的方程为:x2+(y-1)2=16.
故选D.
点评 本题考查抛物线与圆的方程的综合应用,考查转化思想以及计算能力.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
19.设A、B为抛物线y2=2px(p>0)上相异两点,则$|\overrightarrow{OA}+\overrightarrow{OB}{|^2}-|\overrightarrow{AB}{|^2}$的最小值为( )
| A. | -4p2 | B. | -3p2 | C. | -2p2 | D. | -p2 |
20.将正偶数按下边规律排列,第19行,从左到右,第6个数是( )
2
4 6 8
10 12 14 16 18
20 22 24 26 28 30 32
…
2
4 6 8
10 12 14 16 18
20 22 24 26 28 30 32
…
| A. | 654 | B. | 656 | C. | 658 | D. | 660 |
17.若函数f(x)=ax3+bx2+cx+d(a,b,c,d∈R)有极值点,则导函数f′(x)的图象可能是( )
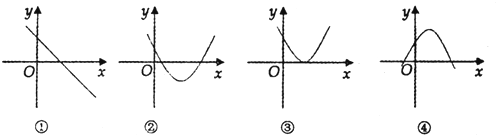

| A. | ①③ | B. | ②③ | C. | ①②④ | D. | ②④ |
14.直线l与抛物线y2=8x交于A、B两点,若线段AB中点的纵坐标为2,则l的斜率等于( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
19.过点A(3,1)作圆(x-2)2+(y-2)2=4的弦,则当弦长最短时弦所在的直线方程为( )
| A. | x+y-4=0 | B. | x-y+2=0 | C. | x+y+4=0 | D. | x-y-2=0 |