题目内容

19．过点A（3，1）作圆（x-2）2+（y-2）2=4的弦，则当弦长最短时弦所在的直线方程为（　　）
A．x+y-4=0B．x-y+2=0C．x+y+4=0D．x-y-2=0

分析 由垂径定理可得，过A点的最短弦所在直线与过A点的直径垂直，由圆的方程求出圆心坐标后，可以求出过A点的直径的斜率，进而求出过A点的最短弦所在直线的斜率，利用点斜式，可以得到过A点的最短弦所在直线的方程．

解答 解：由圆的标准方程（x-2）2+（y-2）2=4，
即圆的圆心坐标为（2，2），
则过A点的直径所在直线的斜率为-1，
由于过A点的最短弦所在直线与过A点的直径垂直
∴过A点的最短弦所在直线的斜率为1，
∴过A点的最短弦所在直线的方程y-1=1（x-3），即x-y-2=0．
故选D．

点评 本题考查的知识点是直线与圆相交的性质，其中由垂径定理，判断出过A点的最短弦所在直线与过A点的直径垂直是解答本题的关键．

练习册系列答案
相关题目
9．以抛物线x2=4y的焦点F为圆心的圆交抛物线于A、B两点，交抛物线的准线于C、D两点，若四边形ABCD是矩形，则圆的方程为（　　）
A．x2+（y-1）2=3B．x2+（y-1）2=4C．x2+（y-1）2=12D．x2+（y-1）2=16
10．已知函数f（x）=（3-a）x-2+a-2lnx（a∈R）．
（Ⅰ）若a≤3，试讨论函数f（x）的单调性；
（Ⅱ）若函数f（x）＞x在（0，$\frac{1}{2}$）上恒成立，求实数a的取值范围．
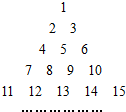7．将全体正整数排成一个三角形数阵：按照如图所示排列的规律：
（1）第7行从左到右的第3个数为24．
（2）第n行（n≥3）从左向右的第3个数为$\frac{{n}^{2}-n+6}{2}$．
14．已知函数f（x）=2sin（ωx+$\frac{π}{6}$）+1+a，（ω＞0），任意相邻两个对称轴之间的距离为$\frac{π}{2}$，
（1）求ω的值并求函数f（x）的单调递增区间；
（2）若方程f（x）=0在$[0，\frac{3π}{4}]$上有两个不同的实根x1，x2，求a的取值范围和x1+x2的值．
4．设正项数列{an}满足：a1=$\frac{1}{2}$，an+1=$\frac{1}{1+an}$，n∈N*．
（1）证明：若an＜$\frac{\sqrt{5}-1}{2}$，则an+1＞$\frac{\sqrt{5}-1}{2}$；
（2）回答下列问题并说明理由：
是否存在正整数N，当n≥N时|an-$\frac{\sqrt{5}-1}{2}$|+|an+1-$\frac{\sqrt{5}-1}{2}$|＜0.001恒成立？
11．已知函数f（x）=x3-x+3．
（Ⅰ）求f（x）在x=1处的切线方程；
（Ⅱ）求f（x）的单调递增区间．
8．已知函数f（x）=$\frac{x}{k}$-lnx（k＞0）
（1）求f（x）的最小值；
（2）若k=2，判断方程f（x）-1=0在区间（0，1）内实数解的个数；
（3）证明：对任意给定的M＞0，总存在正数x0，使得当x＞x0时，恒有$\frac{x}{2}$-lnx＞M．
9．已知函数f（x）=ax+$\frac{a-1}{x}$（a∈R），g（x）=lnx．
（1）若对任意的实数a，函数f（x）与g（x）的图象在x=x0处的切线斜率总相等，求x0的值；
（2）对任意x≥1，不等式f（x）-g（x）≥1恒成立，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网