题目内容
19.设A、B为抛物线y2=2px(p>0)上相异两点,则$|\overrightarrow{OA}+\overrightarrow{OB}{|^2}-|\overrightarrow{AB}{|^2}$的最小值为( )| A. | -4p2 | B. | -3p2 | C. | -2p2 | D. | -p2 |
分析 设A(xA,yA),B(xB,yB).则$|\overrightarrow{OA}+\overrightarrow{OB}{|^2}-|\overrightarrow{AB}{|^2}=4({x_A}{x_B}+{y_A}{y_B})$,分类讨论,结合韦达定理,即可得出结论.
解答 解:设A(xA,yA),B(xB,yB).则$|\overrightarrow{OA}+\overrightarrow{OB}{|^2}-|\overrightarrow{AB}{|^2}=4({x_A}{x_B}+{y_A}{y_B})$,
若直线AB斜率存在,设为y=k(x-a),联立得k2x2-2(ak2+p)x+k2a2=0,
则${x_A}{x_B}={a^2}$,${y_A}{y_B}={k^2}({x_A}-a)({x_B}-a)=-2ap$.$|\overrightarrow{OA}+\overrightarrow{OB}{|^2}-|\overrightarrow{AB}{|^2}=4({a^2}-2ap)=4[{(a-p)^2}-{p^2}]≥-4{p^2}$.
若直线不存在,当${x_A}={x_B}=a\;,\;\;{y_A}=-{y_B}=\sqrt{2ap}$时上式也成立.故所求最小值为-4p2.
当且仅当直线AB过点(p,0)时等号成立.
故选A.
点评 本题考查了抛物线的简单几何性质,考查了学生的计算能力,体现了分类讨论的数学思想方法,是中档题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
11.用正奇数按如表排列
则2017在第 行第 列.( )
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第一行 | 1 | 3 | 5 | 7 | |
| 第二行 | 15 | 13 | 11 | 9 | |
| 第三行 | 17 | 19 | 21 | 23 | |
| … | … | 27 | 25 |
| A. | 第253行第1列 | B. | 第253行第2列 | C. | 第252行第3列 | D. | 第254行第2列 |
9.以抛物线x2=4y的焦点F为圆心的圆交抛物线于A、B两点,交抛物线的准线于C、D两点,若四边形ABCD是矩形,则圆的方程为( )
| A. | x2+(y-1)2=3 | B. | x2+(y-1)2=4 | C. | x2+(y-1)2=12 | D. | x2+(y-1)2=16 |
 一个四棱锥的正视图,侧视图(单位:cm)如图所示,
一个四棱锥的正视图,侧视图(单位:cm)如图所示,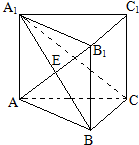 已知ABC-A1B1C1为直三棱柱,AB⊥BC,AA1=AB=BC,连接AB1交A1B于点E,
已知ABC-A1B1C1为直三棱柱,AB⊥BC,AA1=AB=BC,连接AB1交A1B于点E,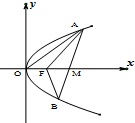 已知抛物线C:y2=2px(p>0),焦点F($\frac{p}{2}$,0),如果存在过点M(x0,0)$({x_0}>\frac{p}{2})$的直线l与抛物线C交于不同的两点A、B,使得S△AOM=λ•S△FAB,则称点M为抛物线C的“λ分点”.
已知抛物线C:y2=2px(p>0),焦点F($\frac{p}{2}$,0),如果存在过点M(x0,0)$({x_0}>\frac{p}{2})$的直线l与抛物线C交于不同的两点A、B,使得S△AOM=λ•S△FAB,则称点M为抛物线C的“λ分点”.