题目内容
18.若△ABC为等腰三角形,∠ABC=$\frac{2}{3}$π,则以A,B为焦点且过点C的椭圆的离心率为$\frac{{\sqrt{3}-1}}{2}$.分析 由题意可知:设AB=BC=1,假设AB在x轴上,设椭圆方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),由余弦定理可知:丨AC丨2=3,则丨AC丨=$\sqrt{3}$,2a=$\sqrt{3}$+1,a=$\frac{\sqrt{3}+1}{2}$,2c=1,c=$\frac{1}{2}$,e=$\frac{c}{a}$=$\frac{\frac{1}{2}}{\frac{\sqrt{3}+1}{2}}$=$\frac{{\sqrt{3}-1}}{2}$,即可求得椭圆的离心率.
解答  解:设AB=BC=1,假设AB在x轴上,设椭圆方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
解:设AB=BC=1,假设AB在x轴上,设椭圆方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
由余弦定理可知:丨AC丨2=丨AB丨2+丨BC丨2-2丨AB丨•丨BC丨•cosB=1+1-2×1×1×(-$\frac{1}{2}$)=3
∴丨AC丨=$\sqrt{3}$,
∵以A、B为焦点的椭圆经过点C,
∴2a=$\sqrt{3}$+1,a=$\frac{\sqrt{3}+1}{2}$,2c=1,c=$\frac{1}{2}$,
∴e=$\frac{c}{a}$=$\frac{\frac{1}{2}}{\frac{\sqrt{3}+1}{2}}$=$\frac{{\sqrt{3}-1}}{2}$,
故答案为:$\frac{{\sqrt{3}-1}}{2}$.
点评 本题考查余弦定理的运用,考查椭圆的几何性质及标准方程的应用,属于基础题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
9.以抛物线x2=4y的焦点F为圆心的圆交抛物线于A、B两点,交抛物线的准线于C、D两点,若四边形ABCD是矩形,则圆的方程为( )
| A. | x2+(y-1)2=3 | B. | x2+(y-1)2=4 | C. | x2+(y-1)2=12 | D. | x2+(y-1)2=16 |
3.已知函数f(x)=ax3+bx2+cx,其导函数为f′(x)的部分值如表所示:
根据表中数据,回答下列问题:
(Ⅰ)实数c的值为6;当x=3时,f(x)取得极大值(将答案填写在横线上).
(Ⅱ)求实数a,b的值.
(Ⅲ)求f(x)的单调区间.
| x | -2 | 0 | 1 | 3 | 8 |
| f′(x) | -10 | 6 | 8 | 0 | -90 |
(Ⅰ)实数c的值为6;当x=3时,f(x)取得极大值(将答案填写在横线上).
(Ⅱ)求实数a,b的值.
(Ⅲ)求f(x)的单调区间.
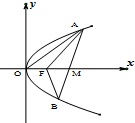 已知抛物线C:y2=2px(p>0),焦点F($\frac{p}{2}$,0),如果存在过点M(x0,0)$({x_0}>\frac{p}{2})$的直线l与抛物线C交于不同的两点A、B,使得S△AOM=λ•S△FAB,则称点M为抛物线C的“λ分点”.
已知抛物线C:y2=2px(p>0),焦点F($\frac{p}{2}$,0),如果存在过点M(x0,0)$({x_0}>\frac{p}{2})$的直线l与抛物线C交于不同的两点A、B,使得S△AOM=λ•S△FAB,则称点M为抛物线C的“λ分点”.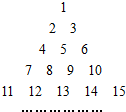 将全体正整数排成一个三角形数阵:按照如图所示排列的规律:
将全体正整数排成一个三角形数阵:按照如图所示排列的规律: