题目内容
17.若函数f(x)=ax3+bx2+cx+d(a,b,c,d∈R)有极值点,则导函数f′(x)的图象可能是( )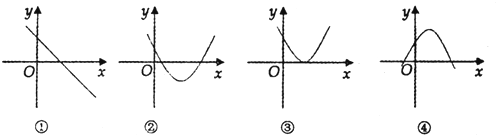
| A. | ①③ | B. | ②③ | C. | ①②④ | D. | ②④ |
分析 由若函数f(x)=ax3+bx2+cx+d(a,b,c,d∈R)有极值点,极值点为f(x0),则函数f′(x)有零点,且在零点左右两侧异号,根据函数图象可知:③f′(x0)=0,但x>x0,x<x0,恒有f′(x0)>0,①②④满足函数f′(x)有零点,且在零点左右两侧异号,即可求得答案.
解答 解:若函数f(x)=ax3+bx2+cx+d(a,b,c,d∈R)有极值点,极值点为f(x0),
则函数f′(x)有零点,且在零点左右两侧异号,
由函数图象可知:③f′(x0)=0,
但x>x0,x<x0,恒有f′(x0)>0,
故③不正确,
①②④满足函数f′(x)有零点,且在零点左右两侧异号,
故选C.
点评 本题考查导数的应用,考查利用导数求函数的单调性及极值的充要条件,考查数形结合思想,属于基础题.

练习册系列答案
相关题目
5.设函数f(x)=x3-4x-a,0<a<2.若f(x)的三个零点为x1,x2,x3,且x1<x2<x3,则( )
| A. | x1<-2 | B. | x2>0 | C. | x3<1 | D. | x3>2 |
2.用与球心距离为1的平面去截球,所得截面圆的面积为π,则球的表面积为( )
| A. | $\frac{8π}{3}$ | B. | $\frac{32π}{3}$ | C. | 8π | D. | $\frac{8\sqrt{2}π}{3}$ |
9.以抛物线x2=4y的焦点F为圆心的圆交抛物线于A、B两点,交抛物线的准线于C、D两点,若四边形ABCD是矩形,则圆的方程为( )
| A. | x2+(y-1)2=3 | B. | x2+(y-1)2=4 | C. | x2+(y-1)2=12 | D. | x2+(y-1)2=16 |
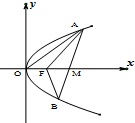 已知抛物线C:y2=2px(p>0),焦点F($\frac{p}{2}$,0),如果存在过点M(x0,0)$({x_0}>\frac{p}{2})$的直线l与抛物线C交于不同的两点A、B,使得S△AOM=λ•S△FAB,则称点M为抛物线C的“λ分点”.
已知抛物线C:y2=2px(p>0),焦点F($\frac{p}{2}$,0),如果存在过点M(x0,0)$({x_0}>\frac{p}{2})$的直线l与抛物线C交于不同的两点A、B,使得S△AOM=λ•S△FAB,则称点M为抛物线C的“λ分点”.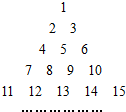 将全体正整数排成一个三角形数阵:按照如图所示排列的规律:
将全体正整数排成一个三角形数阵:按照如图所示排列的规律: