题目内容
生产A,B两种产品,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种产品各100件进行检测,检测结果统计如下:
(Ⅰ)试分别估计产品A、产品B为正品的概率;
(Ⅱ)生产一产品件A,若是正品可盈利50元,若是次品则亏损10元;生产一件产品B,若是正品可盈利100元,若是次品则亏损20元,在(Ⅰ)的前提下:
①求生产5件产品B所获得的利润不少于300元的概率;
②求生产1件产品A和1件产品B所得的总利润为30元或90元的概率.
| 测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 产品A | 8 | 12 | 40 | 32 | 8 |
| 产品B | 7 | 18 | 40 | 29 | 6 |
(Ⅱ)生产一产品件A,若是正品可盈利50元,若是次品则亏损10元;生产一件产品B,若是正品可盈利100元,若是次品则亏损20元,在(Ⅰ)的前提下:
①求生产5件产品B所获得的利润不少于300元的概率;
②求生产1件产品A和1件产品B所得的总利润为30元或90元的概率.
考点:相互独立事件的概率乘法公式,古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)依题意,用每一种产品的正品数除以100,即得该种产品的正品的概率.
(Ⅱ)(1)设生产5件产品B中有x件正品,次品为(5-x)件,根据100x-20×(5-x)≥300其中0≤x≤5. 求得x的取值范围,利用n次独立重复实验中恰好发生k次的概率公式求得所求事件的概率.
(2)生产1件产品A和1件产品B所得的总利润有可能是-30、30、90、150,“所得的总利润为30”表示产品A为正品且产品B为次品,“所得的总利润为90”表示产品A为次品且产品B为正品,由此求得所求事件的概率.
(Ⅱ)(1)设生产5件产品B中有x件正品,次品为(5-x)件,根据100x-20×(5-x)≥300其中0≤x≤5. 求得x的取值范围,利用n次独立重复实验中恰好发生k次的概率公式求得所求事件的概率.
(2)生产1件产品A和1件产品B所得的总利润有可能是-30、30、90、150,“所得的总利润为30”表示产品A为正品且产品B为次品,“所得的总利润为90”表示产品A为次品且产品B为正品,由此求得所求事件的概率.
解答:
解:(Ⅰ)依题意,产品A为正品的概率为
=
;产品B为正品的概率为
=
.
(Ⅱ)(1)设生产5件产品B中有x件正品,次品为(5-x)件,
依题意有100x-20×(5-x)≥300其中0≤x≤5.
解得x≥
即x可能取到4或5
设M=“生产5件产品B所获得的利润不少于300元”,则P(M)=
(
)4(1-
)1+
(
)5=
.
(2)生产1件产品A和1件产品B所得的总利润有可能是-30、30、90、150
“所得的总利润为30”表示产品A为正品且产品B为次品,
“所得的总利润为90”表示产品A为次品且产品B为正品,
设N=“生产1件产品A和1件产品B所得的总利润为30元或90元”,
则P(N)=
×
+
×
=
.
| 80 |
| 100 |
| 4 |
| 5 |
| 75 |
| 100 |
| 3 |
| 4 |
(Ⅱ)(1)设生产5件产品B中有x件正品,次品为(5-x)件,
依题意有100x-20×(5-x)≥300其中0≤x≤5.
解得x≥
| 10 |
| 3 |
设M=“生产5件产品B所获得的利润不少于300元”,则P(M)=
| C | 4 5 |
| 3 |
| 4 |
| 3 |
| 4 |
| C | 5 5 |
| 3 |
| 4 |
| 81 |
| 128 |
(2)生产1件产品A和1件产品B所得的总利润有可能是-30、30、90、150
“所得的总利润为30”表示产品A为正品且产品B为次品,
“所得的总利润为90”表示产品A为次品且产品B为正品,
设N=“生产1件产品A和1件产品B所得的总利润为30元或90元”,
则P(N)=
| 4 |
| 5 |
| 1 |
| 4 |
| 1 |
| 5 |
| 3 |
| 4 |
| 7 |
| 20 |
点评:本题主要考查古典概率及其计算公式的应用,n次独立重复实验中恰好发生k次的概率,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
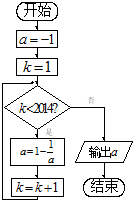
执行如图所示的程序框图所表达的算法,输出的结果为( )

| A、2 | ||
| B、1 | ||
C、
| ||
| D、-1 |