题目内容
已知集合A={x|y=lg（-x2+3x-2）}，集合B={y|y=x2-2x+a，x∈R}
（1）若A∩B≠∅，求实数a的取值范围；
（2）若A∪B=B，求实数a的取值范围．
（1）若A∩B≠∅，求实数a的取值范围；
（2）若A∪B=B，求实数a的取值范围．
考点：并集及其运算,交集及其运算
专题：集合
分析：求出A中x的范围确定出A，求出B中y的范围表示出B，
（1）根据两集合的交集不为空集，确定出a的范围即可；
（2）根据A与B并集为B，得到A为B的子集，确定出a的范围即可．
（1）根据两集合的交集不为空集，确定出a的范围即可；
（2）根据A与B并集为B，得到A为B的子集，确定出a的范围即可．
解答：
解：由A中y=lg（-x2+3x-2），得到-x2+3x-2＞0，
即x2-3x+2＜0，
解得：1＜x＜2，即A=（1，2）；
由B中y=x2-2x+a=（x-1）2+a-1≥a-1，得到B=[a-1，+∞），
（1）∵A∩B≠∅，
∴a-1＜2，即a＜3；
（2）∵A∪B=B，
∴A⊆B，
则a-1≤1，即a≤2．
即x2-3x+2＜0，
解得：1＜x＜2，即A=（1，2）；
由B中y=x2-2x+a=（x-1）2+a-1≥a-1，得到B=[a-1，+∞），
（1）∵A∩B≠∅，
∴a-1＜2，即a＜3；
（2）∵A∪B=B，
∴A⊆B，
则a-1≤1，即a≤2．
点评：此题考查了并集及其运算，熟练掌握并集的定义是解本题的关键．
练习册系列答案
名校通行证有效作业系列答案
相关题目
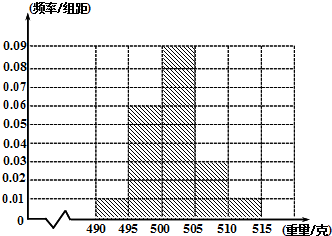某食品厂为了检查甲乙两条自动包装流水线的生产情况，随机在这两条流水线上各抽取40件产品作为样本称出它们的重量（单位：克），重量值落在（495，510]的产品为合格品，否则为不合格品．表1是甲流水线样本频数分布表，如图是乙流水线样本的频率分布直方图．