题目内容
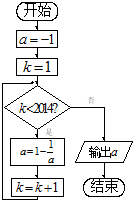
执行如图所示的程序框图所表达的算法，输出的结果为（ ）
| A、2 | ||
| B、1 | ||
C、
| ||
| D、-1 |
考点：程序框图
专题：算法和程序框图
分析：根据框图的流程模拟运行程序，发现a值出现的周期，根据条件确定跳出循环的k值，从而确定输出的a值．
解答：
解：由程序框图知：第一次循环a=1-
=2，k=2；
第二次循环a=1-
=
，k=3；
第三次循环a=1-
=-1，k=4；
第四次循环a=2，k=5．
…，
∴a值出现的周期为3，
又跳出循环的k值为2014，2013=3×671，
∴输出a=-1．
故选：D．
| 1 |
| -1 |
第二次循环a=1-
| 1 |
| 2 |
| 1 |
| 2 |
第三次循环a=1-
| 1 | ||
|
第四次循环a=2，k=5．
…，
∴a值出现的周期为3，
又跳出循环的k值为2014，2013=3×671，
∴输出a=-1．
故选：D．
点评：本题考查了当型循环结构的程序框图，根据框图的流程模拟运行程序发现a值出现的周期及确定跳出循环的k值是解题的关键．
练习册系列答案
相关题目
已知椭圆的中心在原点，长轴长为6，一条准线方程为x=9，则该椭圆的标准方程为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设f（x）=
，若f（0）是f（x）的最小值，则a的取值范围为（ ）
|
| A、[-1，2] |
| B、[-1，0] |
| C、[1，2] |
| D、[0，2] |
结论为：xn+yn能被x+y整除，令n=1，2，3，4验证结论是否正确，得到此结论成立的条件可以为（ ）
| A、n∈N* |
| B、n∈N*且n≥3 |
| C、n为正奇数 |
| D、n为正偶数 |
函数f(x)=lnx+
的零点所在的区间是（ ）
| 1 |
| 2 |
| A、（e-4，e-2） |
| B、（e-2，1） |
| C、（1，e2） |
| D、（e2，e4） |
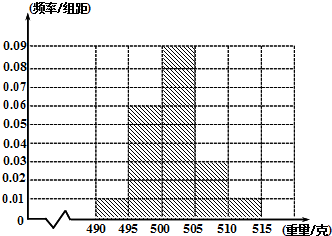某食品厂为了检查甲乙两条自动包装流水线的生产情况，随机在这两条流水线上各抽取40件产品作为样本称出它们的重量（单位：克），重量值落在（495，510]的产品为合格品，否则为不合格品．表1是甲流水线样本频数分布表，如图是乙流水线样本的频率分布直方图．